Na produção de folhas metálicas ou plásticas, é costume resfriar o material antes que ele deixe o processo de produção para armazenamento ou embarque para o cliente. Tipicamente, o processo é contínuo, com uma folha de espessura S e largura W sendo resfriada enquanto transita por uma distância Le com uma velocidade V entre dois rolos. Neste problema, consideramos o resfriamento de uma liga de alumínio (2024-T6) por uma corrente de ar, que se move a uma velocidade «„ no sentido oposto ao da velocidade da folha e sobre a sua superfície superior. Um promotor de turbulência é usado para propiciar um desenvolvimento de camada-limite turbulenta sobre toda a superfície.
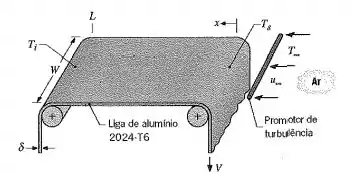
(a) Aplicando a conservação de energia em uma superfície de controle de comprimento dx, que se move com a folha ou é estacionária e através da qual a folha passa, deduza uma equação diferencial que governa a distribuição de temperaturas ao longo da folha. Em função da baixa emissividade do alumínio, os efeitos radiantes podem ser desprezados. Escreva o seu resultado em termos da velocidade, da espessura e das propriedades da folha (V, 8, p,cj, do coeficiente convectivo local hx associado ao escoamento oposto e da temperatura do ar. Para uma temperatura da folha (T') no início do resfriamento conhecida e influência desprezível da velocidade da folha no desenvolvimento da camada-limite, resolva a equação e obtenha uma expressão para a temperatura na saída Ts.
(b) Para 8 = 2mm, V = 0,10 m/s, L= 5 m,W — 1 m, «„ = 20 m/s,T„= 20°Ce T,= 300°C, qual é a temperatura na saída r,?
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! No item a), vamos aplicar a conservação de energia para uma superfície de controle estacionária. Logo, temos que para a entrada e saída:
Integrando essa expressão em função do tempo:
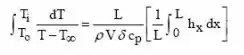
Dessa forma:
Ou seja:
Passo 2
No item b), para as condições descritas,
Dessa forma: