Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 7.Problemas - Ex. 18
Um meio de armazenamento de energia térmica é constituído de uma grande massa de calcário. Ar ambiente é bombeado através de uma fissura no calcário, de 30 mm de altura,5 m de comprimento e 5 m de largura, a uma velocidade de 2 m/s, fornecendo um coeficiente de transferência de calor entre o ar e o calcário dc h = 10 W/(m2 -K). Ao longo de um período de 24 horas, a temperatura na superfície do calcário adjacente à corrente de ar e próximo de sua entrada exibe um comportamento periódico com valores máximo e mínimo de 302 e 298 K, respectivamente.
(a) Determine os valores mínimo e máximo da temperatura do ar próximo à sua entrada.
(b) Determine o fluxo térmico máximo para o ar durante o período de 24 horas próximo à entrada. Determine as temperaturas de entrada e de saída do ar no tempo correspondente ao fluxo térmico máximo no ar.
(c) Determine as temperaturas de saída do ar nos tempos correspondentes às temperaturas de entrada máxima e mínima.
(d) Represente graficamente a temperatura de entrada do ar, a temperatura da superfície do calcário e a taxa de transferência de calor para o calcário durante as 48 horas.
(e) Qual é a espessura de calcário necessária para garantir que o calcário possa ser visto como um meio semi-infinito?
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! O que sabemos das condições iniciais?
Dimensões de uma fissura em calcário. Velocidade do fluxo de ar através da fissura e correspondente coeficiente de convecção. Variação periódica da temperatura superficial do calcário. Bem, consultando a tabela . temos que para o calcário:
Da tabela , ar a 300K:
Analisando, no item a), Para uma variação de temperatura da superfície senoidal, Ts = Ti + ∆T sinωt, o fluxo de calor da superfície é dado pela Equação 5.70:
Aqui, isso deve ser igual ao fluxo de calor por convecção do ar próximo à entrada, ou seja,
Logo,
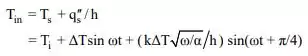
Onde,
Passo 2
(b) O fluxo de calor para o ar é dado por
E isso é máximo quando ωt + π/4 = 3π/2 e sin(ωt + π/4) = -1. Desta forma
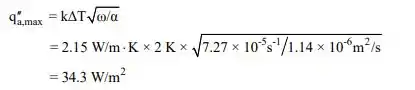
em a = (3π/2 - π/4)/ω = 5,4 × 104 s. Avaliando estanho neste momento a partir da Equação (2) produz
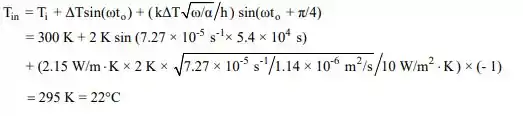
Um balanço de energia em todo o volume de ar na fissura produz (ver Equação 1.11e),
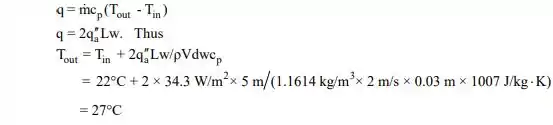
Passo 3
(c) Para encontrar as temperaturas de saída podemos usar a Equação (4), mas precisamos saber da Equação (3). Nas duas vezes indicadas na parte (a),
Assim, da Equação (4)
