Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 7
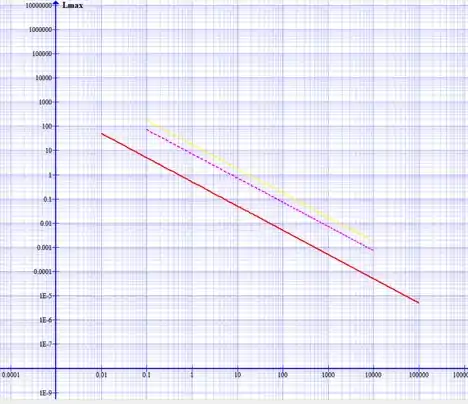
9.7 Trace em um gráfico o comprimento da camada-limite laminar sobre uma placa plana, como uma função da velocidade da corrente livre, para (a) água e ar padrão (b) ao nível do mar e (c) na altitude de 10 km. Use eixos log -log, e calcule valores para o comprimento de camada-limite variando de 0,01 m a 10 m.
Passo 1
a) As condições para água:
Passo 2
Ar padrão
b) Nível do mar:
Passo 3
c) Altitude de 10 km:
Resposta
O plot foi feito usando uma escala log-log, isso explica a as retas. Ar (10km) – Amarelo
Ar ( Nivel do Mar ) – Roxo e Água – Vermelho.
Exercícios de Livros Relacionados
Um pequeno túnel de vento em um laboratório de graduação tem seção de teste quadrada com lado de 305m m . Medições mostram que as camadas limite sobre as paredes do túnel são completamente turbulentas
Tabela 9.1 mostra os resultados numéricos extraídos da solução de Blasius para as equações da camada limite laminar. Trace o gráfico da distribuição de velocidade (note que, da Eq. 9.13, η ≈ 5,0y / δ
Elabore uma análise de custo-benefício para um grande navio petroleiro típico. Determine, como uma porcentagem da carga de petróleo, a quantidade de petróleo que é consumida em um percuso de 3200k m .
Um túnel de vento de laboratório tem uma parede superior móvel que pode ser ajustada para compensar o crescimento da camada limite, dando gradiente de pressão zero ao longo da seção teste. As camadas
Ar de resfriamento é suprido através do canal largo e plano mostrado. Para o mínimo de ruído e perturbação do fluxo de saída, camadas limites laminares devem ser mantidas sobre as paredes do canal. Es