O radiômetro de substituição elétrica, mostrado esquematicamente, determina o poder ótico (radiante) de um feixe através da medida da potência elétrica necessária para aquecer o receptor até a mesma temperatura de quando ele é irradiado. Com um feixe, como um laser de potência ótica , incidente no receptor, a sua temperatura, aumenta ficando superior à temperatura das paredes da câmara, que são mantidas a uma temperatura uniforme . Com o feixe ótico bloqueado, o aquecedor na parte de trás do receptor é energizado e a potência elétrica, , requerida para atingir o mesmo valor de é medida. O objetivo de sua análise é determinar a relação entre as potências elétrica e ótica, considerando processos de transferência de calor no receptor.
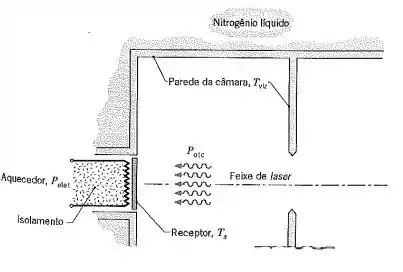
Considere um radiômetro comum receptor com diâmetro de 15 mm, que possui uma superfície enegrecida com uma emissividade de 0,95 e uma absortividade de 0,98 para o feixe ótico. Quando operando no modo ótico, perdas térmicas por condução na parte de trás do receptor são desprezíveis. No modo elétrico, as perdas representam 5% da potência elétrica. Qual é a potência ótica de um feixe quando a potência elétrica indicada é de 20,64 mW? Qual é a temperatura do receptor correspondente?
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora
Conhecemos:
Condições operacionais para um radiômetro de substituição elétrica com a mesma temperatura do receptor, T nos modos elétrico e óptico.
O que devemos encontrar:
Potência óptica do feixe de laser A e temperatura do receptor correspondente quando a potência elétrica indicada é de 20,64 mW.
O esquema e o seguinte:
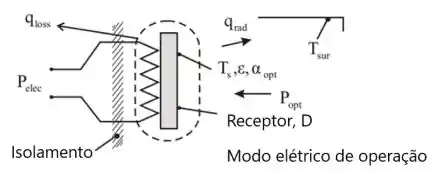
Passo 2
- Constante – Condições de estado
- Condição de perdas na parte traseira do receptor insignificante no modo óptico
- As paredes da câmara formam um grande ambiente isotérmico, efeitos desprezíveis devido à abertura.
- A troca de radiação entre a superfície do receptor e as paredes da câmara ocorre entre pequena superfície e grande invólucro.
- Efeitos de convecção desprezíveis.
Passo 3
A propriedades que temos
Superfície receptora .
A análise que devemos fazer:
O esquema representa as condições de operação para o modo elétrico com o feixe óptico bloqueado, a temperatura da superfície do receptor pode ser encontrada partindo de um balanço de energia no receptor, considerando a entrada de energia elétrica, perda de condução na parte traseira do receptor e o trocador de radiação entre o receptor e a câmara.
Passo 4
Para o modo óptico de operação, a temperatura do feixe óptico incidente no receptor é a mesma do modo elétrico. A potência óptica do feixe pode ser encontrada partindo de um balanço de energia no recepto considerando a potência absorvida do feixe e a troca de radiação entre o receptor e a câmara.
Onde segue do balanço de energia anterior usando
Passo 5
Reconhecendo que a temperatura do receptor e, portanto, a troca de radiação, é a mesma para ambos os modos, um balanço de energia poder ser escrito diretamente em termos da potência óptica absorvida e da potência elétrica equivalente.
“Faça seus medos terem medo de você”

Resposta
Ei, a resposta está no passo a passo :)