Reconsidere o Prob. 2-94. Usando a relação fornecida para o calor gerado na parede, trace a geração de calor como função da distância no intervalo de a e discuta os resultados obtidos. Use EES (ou outro programa).

Nosso primeiro passo é relembrar quem é a função geração de calor da questão anterior. Ela é:

Substituindo os valores, temos:

Agora, vamos analisar o comportamento dessa função no intervalo de até . Com isto, temos o seguinte gráfico:

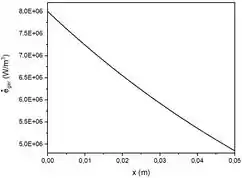
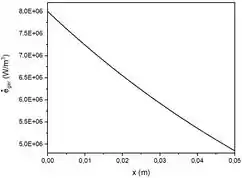
Conforme era esperado, a geração de calor diminui à medida que o valor de aumenta. Isto ocorre, pois a função geração de calor é uma função exponencial com expoente negativo. Logo, ocorre um decaimento.