Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 106
Reconsidere o Prob. 2-105. Usando EES (ou outro programa), trace a taxa de condução de calor através da placa como função da temperatura do lado quente da placa no intervalo de 400 K a 700 K. Discuta os resultados.
Passo 1
Nosso primeiro passo é relembrar qual é a equação que governe a taxa de transferência de calor da questão anterior. Ela é dada por:
Sendo que é o valor da condutividade térmica na temperatura média, que pode ser expresso por:
Como o lado quente é expresso pela temperatura , se substituirmos todos os valores na equação da transferência de calor, com exceção desta temperatura, temos:
Passo 2
Agora que conseguimos determinar a nossa função no passo anterior, precisamos plotar essa função para os valores de variando de 400 K a 700 K. Com isto, temos:
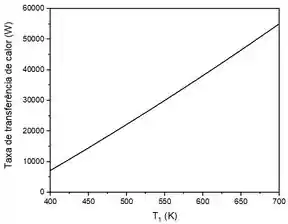
Como era esperado, ao aumentarmos a diferença de temperatura entre as superfícies, aumentamos a taxa de transferência de calor.
Resposta
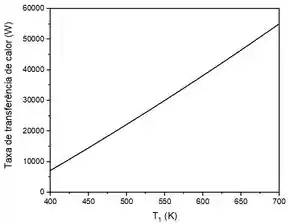
Como era esperado, ao aumentarmos a diferença de temperatura entre as superfícies, aumentamos a taxa de transferência de calor.