Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 42
Considere um bocal convergente e um bocal convergente-divergente com as mesmas áreas de garganta. Para as mesmas condições de entrada, como você compararia as vazões em massa através desses dois bocais?
Passo 1
O enunciado quer que a gente compare a vazão mássica através de dois tipos de bocal diferentes: o bocal convergente e o bocal convergente-divergente. O enunciado supõe que as áreas das gargantas desses bocais são iguais e que o fluido entra nos dois bocais na mesma condição (mesma pressão, temperatura e velocidade). A figura abaixo mostra esses bocais.
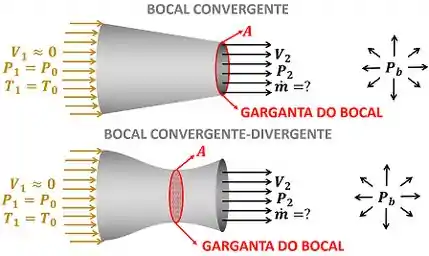
, e são a velocidade, a temperatura e a pressão de entrada do fluido respectivamente. A imagem acima mostra que consideramos a velocidade de entrada do fluido no bocal aproximadamente nula. Substituindo essa informação (de ) nas fórmulas de pressão de estagnação e temperatura de estagnação , achamos que:
, e são a velocidade, a temperatura e a pressão de saída do fluido respectivamente.
é a contrapressão (pressão que o fluido externo na saída do bocal esxerce sobre o escoamento).
No próximo passo vamos entender como comparar essas duas vazões .
Passo 2
Para comparar as pressões nós vamos dividir essa análise em duas partes. A primeira parte é quando a contrapressão é baixa o suficiente para fazer o escoamento na garganta ficar com e o fluido na garganta se mover a velocidade do som .
A segunda parte é quando o escoamento na garganta é subsônico e o fluido se move abaixo da velocidade do som .
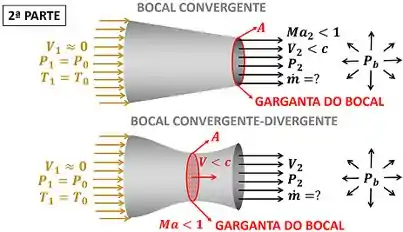
No passo seguinte nós vamos analisar a primeira parte.
Passo 3
Quando o escoamento nas gargantas têm e , a vazão mássica vira:
Como as áreas são iguais para as duas gargantas e as velocidades do som também são iguais, as vazões através dos bocais são iguais!
Ou seja, quando as contrapressões sobre os escoamentos são baixas o suficiente para fazer ficar igual a nas gargantas, as vazões mássicas através dos dois bocais são iguais.
Passo 4
A segunda parte é quando as pressões não são tão baixas para fazer ficar igual nas gargantas. Para esse caso, as pressões na saída dos bocais são iguais a , porque o fluido está em equilíbrio com o meio externo.
A imagem abaixo mostra essa situação.
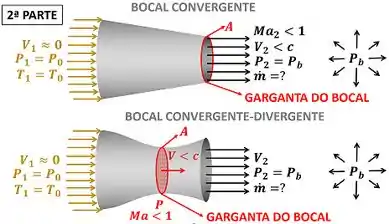
A pressão do fluido na garganta do bocal convergente-divergente é menor que a pressão na garganta do bocal convergente, porque a pressão no difusor aumenta. Logo, a pressão que está na entrada do difusor é maior que a pressão que está na saída do difusor. Isso faz com que a pressão sobre o fluido na saída do bocal seja menor.
Ou seja, o escoamento no bocal convergente-divergente tem uma pressão menor resistindo ao escoamento. Logo, a velocidade do escoamento pela garganta do bocal convergente-divergente é maior que a velocidade do escoamento pela garganta do bocal convergente. Por causa disso, a vazão mássica do bocal convergente-divergente é maior que a vazão mássica do bocal convergente.
Resposta
Quando na garganta dos bocais, as vazões mássicas através dos dois bocais são iguais. Quando na garganta dos bocais, a vazão mássica através do bocal convergente-divergente é maior que a vazão mássica através do bocal convergente.