Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 6
Reconsidere o problema 5. Usando o programa EES (ou outro), investigue o efeito do diâmetro do balão na massa de hélio contida no balão para pressões de:
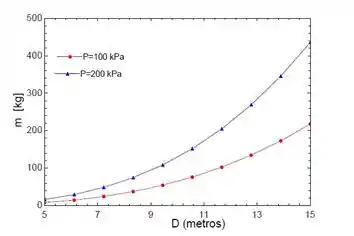
Faça o diâmetro variar de para . Trace o gráfico da massa de hélio versus o diâmetro para ambos os casos
Passo 1
Bora lá! Para resolver essa questão vamos usar o !
Do enunciado da questão 5 a gente vai pegar a temperatura:
Usamos também a constante dos gases ideais :
E pede o número de mols e a massa de hélio presentes no balão. Só que agora a gente vai observar a relação entre a massa do balão e do diâmetro do balão, considerando uma pressão constante.
Em outras palavras funciona assim “Como vai variar o diâmetro do balão se eu aumentar a massa de gás hélio sem aumentar a pressão?”
E vamos fazer isso duas vezes, na primeira e na segunda e em ambos os casos vamos variar a o diâmetro de até . Bora colocar a mão na massa então?!
Passo 2
Com o aberto, vamos colocar nossos dados e as equações que vamos usar para a letra a!
Na parte de “Solução” a gente colocou as equações que vamos utilizar. A primeira é a mesma que a gente utilizou na questão 5 () a única diferença é que a temperatura foi substituida por a gente faz isso pra converter a temperatura de para
A segunda equação é a fórmula que relaciona volume e diâmetro. Estamos considerando aqui que o balão é como uma esfera perfeita:
E por fim a fórmula que da a massa de gás hélio no balão:
No usamos no lugar do porque ai o programa já da pra a gente o valor da massa molar do nosso gás!
Passo 3
Agora vamos fazer a nossa tabelinha com os valores por no gráfico!
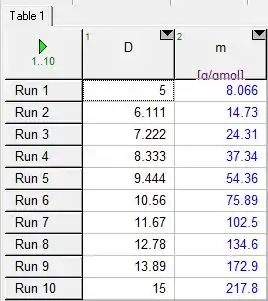
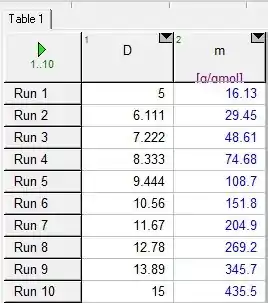
Aqui usamos 10 valores de até , como aquestão pediu! Agora vamos montar a tabela pra letra b. Para isso temos que alterar a pressão nos dados, de para
Agora é só montar a tabela:
E por fim, plotar o gráfico:
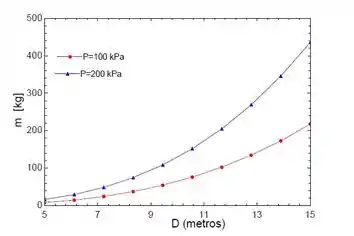
Resposta
