Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 33
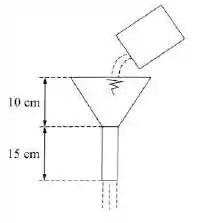
Ao repor o óleo de um motor no posto de serviços,, o frentista mantém o funil sempre constantemente cheio. Como o óleo tem uma elevada viscosidade cinemática supõe-se que o escoamento no funil seja laminar e neste caso, sabe-se que o coeficiente de perda de carga distribuída é dado por . Admite-se que no escoamento não haja perdas singulares importantes e que a perda de carga distribuída acontece somente no trecho cilíndrico do funil, cujo diâmetro é
- Quanto tempo levará para repor o óleo, supondo que o carter do motor tenha capacidade para ?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O tempo necessário para encher o carter é de:
Como temos o volume do carter, podemos encontrar sua vazão a partir de:
Precisamos então determinar a velocidade com que o óleo sai do funil. Temos que:
Passo 2
Podemos encontrar uma expressão para , de acordo com o que foi fornecido pelo exercício:
Portanto, teremos:
Simplificando, temos que:
Substituindo os valores conhecidos, temos que:
Passo 3
Comparando as cargas manométricas no inicio e no fim do escoamento, temos que:
Substituindo os valores, temos que:
Desenvolvendo, encontraremos:
Resolvendo por baskara, encontraremos:
Passo 4
A vazão será:
Logo, o tempo será:
Passo 5
Para verificar se o escoamento é laminar, devemos calcular o número de Reynolds:
Substituindo o valor da velocidade encontrado no passo anterior, temos que:
Como o número de Reynolds é menor que o escoamento é laminar.