Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 72

Um fluido biológico escoa a uma vazão mássica de m ˙ =   0,02   k g / s através de uma serpentina com parede delgada e 5   m m de diâmetro. A serpentina encontra-se submersa em um grande banho de água mantido a 50 ° C . O fluido entra na serpentina a uma temperatura de 25 ° C .

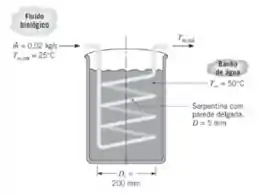
( a ) Estime o comprimento da serpentina e o número de voltas necessárias para fornecer uma temperatura do fluido biológico na saída de T m , s a i   =   38 ° C . Suponha que o banho de água seja um meio quiescente infinito, que a serpentina se aproxime de um tubo horizontal e que o fluido biológico tenha propriedades termo físicas iguais às da água.

( b ) A vazão através da serpentina é controlada por uma bomba cuja vazão bombeada varia aproximadamente ± 10 % em qualquer condição operacional. Essa situação preocupa o engenheiro de projetos, uma vez que a variação correspondente na temperatura de saída do fluido biológico pode influenciar o processo a jusante. Qual variação em T m , s a i você esperaria com uma mudança de ± 10 % em ?

Passo 1

Bom, precisamos ir com calma nesse exercício, pois temos muitas condições de contorno para a física do problema.

Inicialmente o exercício pede para estimarmos o comprimento da serpentina e o número de voltas para fornecer uma temperatura de saída estabelecida.

Logo, devemos ter em mente que devemos focar nas propriedades geométricas de nossa serpentina.

Em escoamento interno em tubos, iniciamos a analise conhecendo-se a direção do fluxo, na qual, para esse exercício ocorre de fora pra dentro, pelo diferencial de temperatura existente.

Passo 2

Dados para fonte fria ou fluido interno, da tabela A-6 Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed. Através de uma temperatura média entre entrada e saída:

T m = T m , e n t r a d a + T m , s a i d a 2 = ( 25 + 273 ) + ( 38 + 273 ) 2 = 304,5 K

Portanto...

c p = 4178 J K g ∙ K ,   μ i = 7,776 × 10 - 4 N ∙ s m 2 ,   k i = 0,6193 W m ∙ K , P r i = 5,263

Dados para fonte quente ou fluido externo, da tabela A-6 Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed. Através de uma temperatura de filme:

T f = T s + T ∞ 2

Note que não possuímos uma temperatura superficial da serpentina, logo devemos estimar, uma dica é que sabemos que o fluxo se dá do externo para o interno, logo só utilizarmos um valor de T s < T ∞ , como por exemplo T s = 35,4 .

T f = 50 + 273 + 35,4 + 273 2 = 315,7   K

Portanto...

k e = 0,635 W m ∙ K ,   P r e = 4,11   ,   υ e = 6,294 × 10 - 7 m 2 s ,   α e = 1,533 × 10 - 7 m 2 s ,   β e = 4,054 × 10 - 4 K - 1

Para o nosso T s = 308,4   K , iremos precisar de:

μ s = 7,28 × 10 - 4 N ∙ s m 2

Passo 3

Agora podemos começar a realizar a formulação, como o fluxo se dá do externo para o interno, temos que T ∞ é nossa referência, e quando isso corre, utilizamos a equação abaixo:

T ∞ - T m , s T ∞ - T m , e = exp ⁡ - U - A s m ˙ c p

Rearranjando, teremos o que chamamos de equação de projeto:

U - A s = - m ˙ c p ln ⁡ T ∞ - T m , s T ∞ - T m , e

U - A s = - 0,02 k g s 4178 J k g ∙ K × ln ⁡ 50 - 38 50 - 25 = 61,3 W K

Passo 4

Agora, acabamos de desvendar o problema, pois temos um dos parâmetros que precisamos, o comprimento:

A s = π D L

Para prosseguirmos com o exercício, será necessário calcular o coeficiente global de transferência de calor, que é igual ao somatório do inverso das resistências.

Do enunciando temos que as paredes são delgadas, logo podemos desprezar a condução e simplesmente considerar a convecção interna e externa, ou seja, teremos a seguinte formulação:

U - A = ∑ 1 1 h A

U - = 1 1 h i - + 1 h e -

Passo 5

Para determinarmos h i , precisamos determinar como o fluido se encontra internamente, ou seja, calcular o R e D , i ...

R e D , i = 4 m ˙ π D μ i = 4 × 0,02 k g s π × 0,005   m 777,6 × 10 - 6 N ∙ s m 2 = 6650

Note que 2300 < R e < 10000 , logo devemos recalcular nosso R e , pois ele se encontra em transição, utilizando a formulação para um fluxo em um tubo espiralado abaixo:

R e D , i , c r i t i c o = R e D , c r 1 + 12 D D c 0,5 = 2300 × 1 + 12 0,005   m 0,2   m 0,5 = 6664

Logo, a correlação correspondente será:

N u - D , i = 3,66 + 4,343 a 3 + 1,158 R e D , i D D c 0,5 b 1,5 1 3 μ i μ s 0,14  

Onde...

a = 1 + 957 D c D R e D , i 2 P r i  

b = 1 + 0,477 P r i

Passo 6

Substituindo os valores:

a = 1 + 957 0,2   m 0,005   m 6650 2 5,263 = 1,0002

b = 1 + 0,477 5,263 = 1,09

N u - D , i = 3,66 + 4,343 1,0002 3 + 1,158 6650 0,005   m 0,2   m 0,5 1,09 1,5 1 3 7,776 × 10 - 7 N ∙ s m 2 7,28 × 10 - 4 N ∙ s m 2 0,14

N u - D , i = 32,8

Logo...

N u - D , i = 32,8 = h - i k i D

h - i = 32,8 0,6193 W m ∙ K 0,005   m = 4065 W m 2 ∙ K

Passo 7

Para determinamos o coeficiente de convecção externo, temos que determinar o Rayleigh, visto que do enunciado, pede-se para se aproximar para um tubo horizontal, onde a correlação correspondente é:

N u - D , e = h - e D k e = 0,60 + 0,387 R a D 1 6 1 + 0,559 P r 9 16 8 27 2

E...

R a D , e = g β e T ∞ - T - s D 3 υ e α e

Onde T - s é a média da temperatura interna com a externa, pela serpentina possuir uma parede delgada, iremos aproximar para T - f .

Logo...Substituindo valores:

R a D , e = 9,81 m s 2 4,054 × 10 - 4 K - 1 315,7 - ( 273 + 50 ) ( 0,005   m ) 3 6,294 × 10 - 7 m 2 s 1,533 × 10 - 7 m 2 s = 7,52 × 10 4

N u - D , e = 0,60 + 0,387 7,52 × 10 4 1 6 1 + 0,559 4,11 9 16 8 27 2 = 9,7

h - e = 9,7 0,635 W m ∙ K 0,005   m = 1231,9   W m 2 ∙ K

Passo 8

Muito bem, agora voltando para o nosso coeficiente de coeficiente global...

U - = 1 1 h i - + 1 h e - = 1 4065 W m 2 ∙ K + 1 1231,9 W m 2 ∙ K - 1 = 945   W m 2 ∙ K  

Logo, o comprimento será:

L = U - A s U - π D = 61,3 W K 945   W m 2 ∙ K ( π ) ( 0,005   m ) = 4,13   m

Definindo, o número de voltas:

N = L π D c = 4,13   m π 0,200   m = 6,67 ≈ 7

Resposta

O comprimento será:

L = 4,13   m

O número de voltas:

N = 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma janela vertical de painel duplo é constituída por duas lâminas de vidro separadas por um espaçamento de 1,2 cm com ar à pressão atmosférica. As temperaturas das superfícies dos vidros através do e
Um objeto quente suspenso por uma corda deve ser resfriado por convecção natural em fluidos cujos volumes mudam de maneira diferente com a temperatura à pressão constante. Em qual fluido a taxa de res
Uma janela vertical de painel duplo de 0,9 m de altura e 1,5 m de largura é constituída por duas lâminas de vidro separadas por um espaçamento de 2,0 cm, com ar à pressão atmosférica. Considerando que
As claraboias são comumente usadas em residências e instalações de produção, uma vez que deixam a luz natural entrar durante o dia, reduzindo, assim, os custos de iluminação. No entanto, oferecem pouc
Um tubo horizontal de 4 m de comprimento e 5 cm de diâmetro onde escoa refrigerante passa através da sala a 20°C. O tubo não é bem isolado, e a temperatura da superfície externa do tubo é -10°C. A emi