Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 30
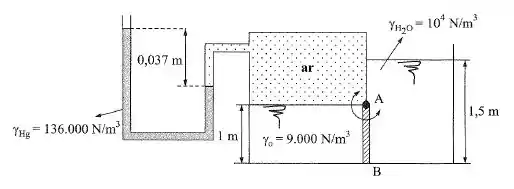
O reservatório da figura possui uma parede móvel , articulada em . Sua largura é e está em equilíbrio nas condições indicadas. Calcular:
- A força que age na face direita da comporta devido à água;
- A força que deve ser aplicada em para que seja mantido o equilíbrio.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O item “a” nos pede a força que age na face direita da comporta devido à água. Vamos chamar essa força de .
Sabemos que a água exerce uma pressão sobre a parede formando um prisma de pressão sobre a comporta. Observe o diagrama abaixo:
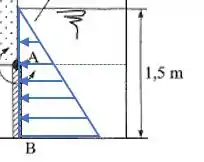
Pela teoria a força provocada na parede é igual ao volume do prisma de pressão gerado pela água.
Se observarmos bem, o prisma de pressão que diz respeito à parte da comporta é um prisma trapezoidal. O volume de um prisma trapezoidal é dado por:
Portanto, aplicando ao problema, temos que:
Onde seria a base menor, a base maior, a altura igual a e a largura igual a . Substituindo os valores e resolvendo, temos que:
Passo 2
O item “b” nos pede a força necessária em para manter o sistema em equilíbrio. Primeiro vamos descobrir a pressão do ar.
A pressão do ar é obtida a partir da análise da escala de mercúrio. Ela equivale ao nível de de mercúrio. Logo:
Agora que vem a sacada da questão. Quanto de óleo formaria uma pressão desta magnitude?
Temos que:
Ou seja, uma coluna de de óleo equivale à pressão do ar no reservatório. Então podemos representar o nosso sistema da seguinte forma:
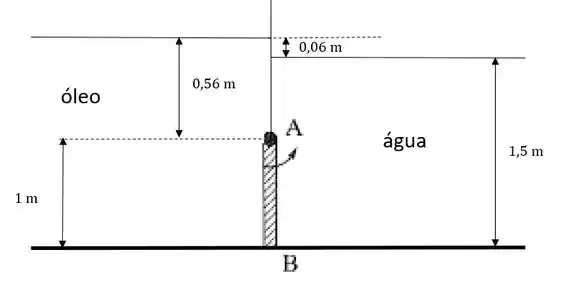
Passo 3
Temos então a seguinte situação:
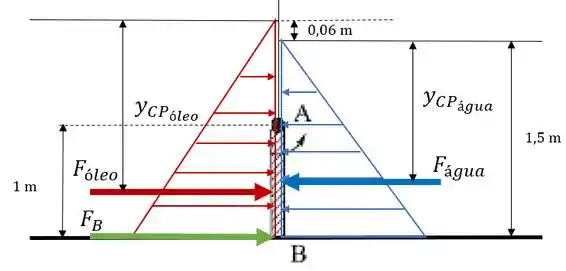
Podemos encontrar a força provocada pelo óleo assim como encontramos a força provocada pela água no item “a”. Temos que:
Passo 4
Sabemos que o somatório de momentos em deve ser nulo. Para aplicar o somatório de momentos e descobrir , temos que saber as alturas dos centros de aplicação das forças.
A equação do centro de pressão é dada por:
Vamos aplicar para cada caso. Sabendo que:
Que é a medida do topo do nível da água até o centro de gravidade, no caso metade, da comporta.
Temos também que:
Como estamos trabalhando para a mesma comporta, os momentos de inércia em cada cálculo serão iguais. Temos que:
Ou seja:
A área será:
Passo 5
Portanto, teremos que:
E:
Passo 6
Agora que sabemos os centros de aplicação das respectivas forças, podemos aplicar o somatório de momentos em e encontrar . Temos que:
Portanto: