Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 29

A comporta da figura, em forma de 1 4 de cilindro, tem peso desprezível. Determinar a relação γ 1 / γ 2 entre os pesos específicos dos líquidos, para que a comporta não gire em torno do ponto O . Dado: x C G = 4 3 R π

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Pela teoria sabemos que a força em uma superfície curva pode ser decomposta em horizontal e vertical como mostrado no diagrama abaixo:

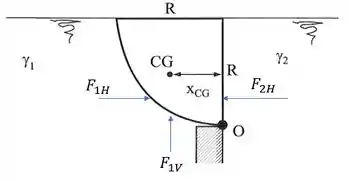
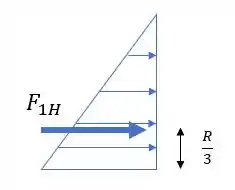
A componente horizontal é igual a força que age na projeção horizontal da superfície curva.

A componente vertical é igual ao peso do fluido imaginário referente ao quarto de círculo da comporta:

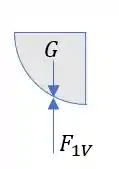
A força F 2 H se comporta como F 1 H .

Passo 2

Como a comporta está em equilíbrio, o somatório de momentos no ponto de articulação O deve ser nulo. Logo:

F 1 H R 3 + F 1 V x C G = F 2 H R 3

O centro de gravidade x C G de um quarto de círculo é:

x C G = 4 R 3 π

Portanto:

F 1 H R 3 + F 1 V 4 R 3 π = F 2 H R 3

Sabemos que:

F 1 H = P C G 1 A 1

F 2 H = P C G 2 A 2

E:

F 1 V = G 1

Portanto:

P C G 1 A 1 R 3 + G 1 4 R 3 π = P C G 2 A 2 R 3

Passo 3

Agora é só desenvolver:

P C G 1 A 1 R 3 + G 1 4 R 3 π = P C G 2 A 2 R 3

γ 1 h C G 1 A 1 + G 1 4 π = γ 2 h C G 2 A 2

γ 1 R 2 R w + γ 1 π R 2 4 w 4 π = γ 2 R 2 R w

Simplificando, temos que:

γ 1 2 + γ 1 = γ 2 2

γ 1 γ 2 = 1 3

Resposta

γ 1 γ 2 = 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os balões normalmente são cheios com gás hélio porque ele tem apenas um sétimo do peso do ar sob condições idênticas. A força de flutuação, que pode ser expressa como F b = ρ a r g V b a l ã o ã , emp
A metade inferior de um contêiner cilíndrico com 10m de altura é preenchida com água ( ρ = 1000k g / m 3 ) e a metade superior com óleo que tem gravidade específica de 0,85 . Determine a diferença de
Ao medir diferenças de pressão pequenas com um manômetro, quase sempre um braço do manômetro é inclinado para melhorar a exatidão da leitura. (A diferença de pressão ainda é proporcional à distância v
Defina a força hidrostática resultante que age em uma superfície submersa e o centro da pressão.
Uma pedra de granito de 170k g ( ρ = 2.700k g / m 3 ) é solta em um lago. Um homem mergulha e tenta erguer a pedra. Determine quanta força o homem precisa aplicar para levantá-la do fundo do lago. Voc