Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 64

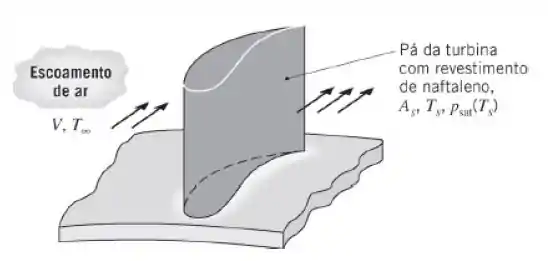
Seja a aplicação da técnica de sublimação do naftaleno (Problema 6.63) em uma pá de turbina a gás que é coberta com naftaleno e tem uma área superficial de A s   =   0,05   m ² . Para determinar o coeficiente de transferência de calor por convecção médio para uma condição de operação representativa, um experimento é efetuado no qual a pá revestida é exposta por 30 min ao ar atmosférico a uma velocidade desejada e a uma temperatura de T ∞   =   27 ° C . Durante o experimento a temperatura da superfície é de T s   =   27 ° C e no seu final a massa da pá está reduzida em Δ m   =   8   g . Qual é o coeficiente de transferência de calor por convecção médio associado à condição de operação?

Passo 1

Boom turminha, vamos seguindo, ok?

Nós queremos achar o coeficiente de transferência de calor por convecção médio associado à condição de operação, não é?

Para isso nós podemos usar a relação:

h - h m - = ρ c p L e ( 1 - n )

Onde ρ é a densidade, c p o calor específico a pressão constante, L e o número de Lewis.

O número de Lewis também pode ser escrito como:

L e = α D A B

Onde α é a difusividade térmica e D A B a difusividade mássica!!

Para a maioria das aplicações n = 1 3 :

h - h m - = ρ c p α D A B 1 - 1 3

h - = h m - ρ c p α D A B 2 3

Na Tabela A.4 para nossa temperatura de 300 K nós temos:

ρ = 1,161 k g m 3

c p = 1007 J k g K

α = 22,5 × 10 - 6 m 2 s

E na Tabela A.8 para o naftaleno e o ar:

D A B = 0,62 × 10 - 5 m 2 s

Então nós só precisamos achar o h m - , não é?

Passo 2

E para acha-lo nós podemos usar a equação:

n A = h m - A s ρ A ,   s - ρ A ,   ∞

h m - = n A A s ρ A ,   s - ρ A ,   ∞

Se lembrarmos que:

n A = ∆ m ∆ t = 0,00 8   k g 30   m i n × 60   s 1   m i n = 4,44 × 10 - 6 k g s

A s   =   0,05   m ²

ρ A ,   ∞ = 0 k g m 3

Então a única coisa que precisamos achar é ρ A ,   s , fácil não é?

Basta nós lembrarmos de usar a equação para os gases ideais, ok?

p A ,   s a t V A = R T s

Se:

V A = M ρ A

Portanto:

p A ,   s a t M ρ A , = R T s

Isolando a densidade:

ρ A = M p A ,   s a t R T s

Lembrando que:

M   =   128,16 k g k m o l

p A , s a t   = 1,33   ×   10 - 4   b a r

T s = 300 K

R = 0,08 314 m ³ . b a r k m o l K

Substituindo:

ρ A , s = 128,16 k g k m o l 1,33   ×   10 - 4   b a r 0,08314 m ³ . b a r k m o l K 300   K = 6,83 × 10 - 4 k g m 3

Achando o coeficiente:

h m - = 4,44 × 10 - 6 k g s 0,05   m ² 6,83 × 10 - 4 k g m 3 = 0,13 m s

Passo 3

E agora o que nós vamos fazer é colocar todos os nossos dados na equação do Passo 1:

h - = 0,13 m s 1,161 k g m 3 1007 J k g K 22,5 × 10 - 6 m 2 s 0,62 × 10 - 5 m 2 s 2 3

h - = 359 W m 2 K

Legal não foi?

Resposta

h - = 359 W m 2 K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma unidade de produção, os componentes de aço devem ser endurecidos por difusão de carbono. Você realizaria o processo de endurecimento à temperatura ambiente ou em um forno a uma temperatura ele
Determine a fração da massa máxima de bicarbonato de cálcio [ C a H C O 3 2 ) ] na água a 350K .
A lei de Fick da difusão é expressa nas bases mássica e molar como m ˙ d i f , A = - ρ A D A B d w A / d x e N ˙ d i f , A = - C A D A B ( d y A / d x ) , respectivamente. Os coeficientes de difusão
O que as ( a ) reações homogêneas e ( b ) reações heterogêneas representam na transferência de massa? A que correspondem na transferência de calor?
Tanto a lei de Fourier da condução de calor quanto a lei de Fick da difusão de massa podem ser expressas como Q ˙ = - k A ( d T / d x ) . O que as quantidades Q ˙ , k , A e T representam na ( a ) cond