Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 59

Um objeto de forma irregular possui um comprimento característico L = 1 m e tem a sua superfície mantida a uma temperatura uniforme T s   =   325   K . Ele encontra-se suspenso em uma corrente de ar a pressão atmosférica ( p   =   1   a t m ) , que tem uma velocidade V   =   100 m s e uma temperatura T ∞   =   275   K . O fluxo térmico médio da superfície para o ar é de 12.000 W m 2 . Chamando a situação anterior de caso 1, analise os casos a seguir e determine se as condições são análogas às do caso 1. Cada caso envolve um objeto com a mesma forma, que está suspenso em uma corrente de ar da mesma maneira. Quando houver comportamento análogo, determine o valor correspondente do coeficiente convectivo médio.

  1. Os valores de T s ,   T ∞ e p permanecem os mesmos, porém L = 2 m e   V   =   50 m s .
  2. Os valores de T s e T ∞ permanecem os mesmos, porém L = 2 m, V   =   50 m s e p = 0,2 atm.
  3. A superfície é coberta por uma película de um líquido que evapora para o ar. Todo o sistema se encontra a 300 K e o coeficiente de difusão da mistura ar-vapor é D A B   =   1,12   ×   10 - 4 m 2 s . Também, L = 2 m, V   =   50 m s e p = 1 atm.
  4. A superfície é coberta por uma outra película de líquido, para o qual D A B =   1,12   ×   10 - 4 m 2 s , e o sistema está a 300 K. Nesse caso, L = 2 m, V   =   250 m s e p = 0,2 atm.

Passo 1

E ai galerinha bonitaaa!!

Animados para mais uma??

Antes nós vamos fazer uma tabela com os nossos casos:

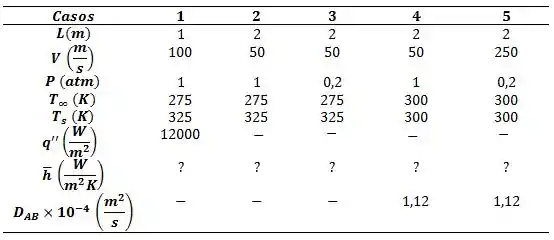
No caso 1 nós precisamos calcular apenas o coeficiente de calor convectivo médio, certo?

Sabendo que:

q ' ' = h - T s - T ∞

Basta nós substituirmos, não é?

12000 W m 2 = h - 325   K - 275   K

h - = 240 W m 2 K

Para saber se as condições dos próximos casos serão análogas ou não precisamos calcular o R e L e o P r :

R e L , 1 = V 1 L 1 v 1

Olhando a Tabela 4 nós temos que para o ar à 300 K e 1 atm:

v 1 = 15 , , 89 × 10 - 6 m 2 s

P r 1 = 0,71

k 1 = 0,0263 W m 2 K

Substituindo nossos dados:

R e L , 1 = 100 m s 1   m 15,89 × 10 - 6 m 2 s = 6,29 × 10 6

Então, para que os casos sejam análogos eles devem apresentar R e L = 6,29 × 10 6 e P r = 0,71 , ok?

Passo 2

No caso 2 nós precisamos calcular o número de Reynolds novamente, não é?

R e L , 2 = 50 m s 2   m 15,89 × 10 - 6 m 2 s = 6,29 × 10 6

Como a temperatura e a pressão permanecem a mesma, P r 1 = 0,71 .

E o que nós temos aqui ?? Um caso análogo ao Caso 1, certo?

Se é assim:

N u 1 - = N u 2 -

Lembrando que:

N u - = h - L k

Colocando na igualdade e isolando nosso coeficiente desejado:

h 2 - L 2 k 2 = h 1 - L 1 k 1

h 2 - = h 1 - L 1 k 1 × k 2 L 2

Como o objeto não vai mudar:

h 2 - = h 1 - L 1 L 2

Substituindo:

h 2 - = 240 W m 2 K 1   m 2   m

h 2 - = 120 W m 2 K

Passo 3

No caso 3, quando a P = 0,2   a t m :

v 3 = 79,45 × 10 - 6 m 2 s

P r 3 = 0,71

Calculando o número de Reynolds:

R e L , 3 = 50 m s 2   m 79,45 × 10 - 6 m 2 s = 1,26 × 10 6

Como nós achamos R e L , 3 ≠ R e L , 1 eles não são análogos!!

Passo 4

Vamos pular pro Caso 4?

Aqui nós temos as mesmas condições do Caso 2, o que nos permite concluir que:

R e L , 1 = R e L , 4

Mas neste caso em especial, para que o caso seja análogo vai precisar haver a igualdade entre:

P r 1 = S c 4

Sabendo que:

S c 4 = v 4 D A B ,   4

E que:

v 4 = v 1 = 15 , , 89 × 10 - 6 m 2 s

Então:

S c 4 = 15 , , 89 × 10 - 6 m 2 s 1,12 × 10 - 4 m 2 s = 0,142

Portanto, P r 1 ≠ S c 4 !!

E o caso 4 também não é análogo !!

Passo 5

Finalizamos com o Caso 5!!

Aqui nós temos a mesma pressão que o Caso 3:

v 5 = 79,45 × 10 - 6 m 2 s

P r 5 = 0,71

Calculando Reynolds:

R e L , 5 = 250 m s 2   m 79,45 × 10 - 6 m 2 s = 6,29 × 10 6

Mas não vai comemorando ainda, para que o caso seja análogo vai precisar haver a igualdade entre:

P r 1 = S c 5

Sabendo que:

S c 5 = v 5 D A B ,   5 = 79,45 × 10 - 6 m 2 s 1,12 × 10 - 4 m 2 s = 0 , 71

Satisfazendo a igualdade, certo?

Então o que nós temos aqui é um segundo caso análogo ao Caso 1, certo?

Se é assim:

N u 1 - = N u 5 -

h 5 - L 5 D A B ,   5 = h 1 - L 1 k 1

h 5 - = h 1 - L 1 k 1 × D A B ,   5 L 5

Substituindo:

h 5 - = 240 W m 2 K 1   m 0,0263 W m K × 1,12 × 10 - 4 m 2 s 2   m

h 5 - = 0 , 51 m s  

Concluindo:

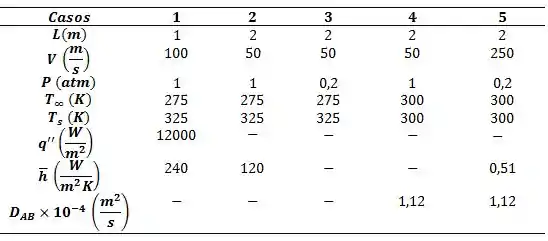
Legal, não foi?

Resposta

  1. h - = 12 0 W m 2 K
  2. N ã o   é   a n á l o g o ;
  3. N ã o   é   a n á l o g o ;
  4. h - = 0,51 m s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma camada de água, com 2m m de espessura, sobre uma placa eletricamente aquecida é mantida a uma temperatura de T a = 340K , enquanto ar seco a T ∞ = 300K escoa sobre a sua superfície (caso A). O con
Um experimento é conduzido para determinar o coeficiente de transferência de massa por convecção médio em uma pequena gota usando um aquecedor controlado para operar a uma temperatura constante. O his
Em um dia de verão, a temperatura do ar é de 27 ° C e sua umidade relativa é de 30%. Água evapora da superfície de um lago a uma taxa de 0,10k g / m 2 ⋅ h por metro quadrado de área da sua superfície.
A taxa na qual água é perdida devido à evaporação em uma superfície de um corpo de água pode ser determinada através da medida da taxa de variação do seu nível. Considere um dia de verão no qual as te
É observado que uma panela com 230m m de diâmetro contendo água a 23 ° C apresenta uma taxa de perda de massa de 1,5 × 10 - 5k g / s , quando o ar ambiente está seco e a uma temperatura de 23 ° C .a)