Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 114

Seja o escoamento de ar através de um tubo de aço com pequenos diâmetros. Represente graficamente o número de Nusselt associado ao escoamento laminar plenamente desenvolvido, com fluxo na superfície constante, para diâmetros de tubos variando de 1 μm ≤ D ≤ 1 mm. Avalie

as propriedades do ar a T = 350 K e a pressão atmosférica. Os coeficientes de acomodação térmica e de momento são α t = 0,92 e α p = 0,87, respectivamente. Compare os números de Nusselt aqui calculados com o valor fornecido na Equação 8.53, NuD = 4,36.

Passo 1

Beleza! Vamos começar o exercício pegando as propriedades do ar na pressão atmosférica a uma temperatura de 350 K. Para isso, vamos recorrer a tabela A.4 do apêndice A, onde conseguimos as seguintes propriedades:

c p = 1009   k J / k g . K

P r = 0,70

k = 0,03   W / m . K

M = 28,97   k m o l / k g

Agora, nós vamos recorrer à figura 2.8 vista no capítulo 2, onde poderemos pegar os valores dos diâmetros moleculares, então temos:

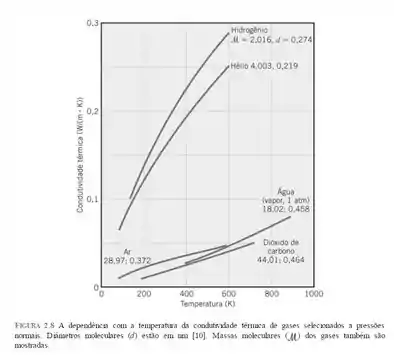
Com ela, podemos ver que o diâmetro molecular do ar será:

d = 0,372   n m

Agora, sabemos também que a constante de gás ideal para o ar é dada por:

R = 0,287   k J / k g . K

Então, com isso, podemos calcular o calor específico a volume constante, onde teremos:

c v = c p - R = 1,007 - 0,287 → c v = 0,720   k J / k g . K

E, agora podemos calcular a razão entre os calores específicos, dado por:

γ = c p c v = 1,007 0,287 → γ = 1,4

Passo 2

Agora nós vamos recorrer à equação do livre percurso médio, dado pela equação 2.11, onde temos:

λ l p m = k B T 2 π d 2 p

Sabendo que a constante de Boltzmann é dada por k B = 1,381.10 - 23   J / K , então, substituindo os valores conhecidos nessa equação, teremos:

λ l p m = 1,381.10 - 23 350 2 π 0,372.10 - 9 2 1,01.10 5 → λ p l m = 77,8.10 - 9   m

Agora, nós podemos encontrar o número de Nusselt através da equação 8.78a:

N u D = h D k = 48 11 - 6 ξ + ξ 2 + 48 Γ t

Onde temos Γ t dado por:

Γ t = 2 - α t α t . 2 γ γ + 1 λ l p m P r D

E que ξ é dado por:

ξ = 8 Γ p 1 + 8 Γ p

E, por sua vez, Γ p é dado por:

Γ p = 2 - α p α p λ p l m D

Passo 3

Então vamos começar calculando a expressão para Γ p :

Γ p = 2 - 0,87 0,87 77,8.10 - 9 D → Γ p = 101.10 - 9 D

Agora calculando a expressão para ξ , temos:

ξ = 8 Γ p 1 + 8 Γ p = 8 101.10 - 9 D 1 + 8 101.10 - 9 D

E, por fim a expressão para Γ t :

Γ t = 2 - α t α p . 2 γ γ + 1 λ l p m P r D = 2 - 0,92 0,87 2 1,4 1,4 + 1 77,8.10 - 9 0,7 D → Γ t = 152 . 10 - 9 D

Então, substituindo essas expressões na equação para Nusselt, temos:

N u D = 48 11 - 6 ξ + ξ 2 + 48 Γ t

N u D = 48 11 - 6 8 101.10 - 9 D 1 + 8 101.10 - 9 D + 8 101.10 - 9 D 1 + 8 101.10 - 9 D 2 + 48 152 . 10 - 9 D

Então, com essa expressão, conseguimos obter o gráfico a seguir de Nusselt em função do diâmetro:

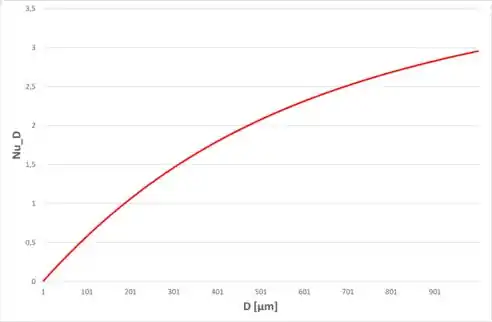
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o desenvolvimento de uma camada-limite térmica laminar próxima a entrada do tubo mostrado na Figura 8.4. Quando a camada-limite fluidodinâmica é fina em relação ao diâmetro do tubo, a região
Uma vazão de 0 , 2 5k g / s de mercúrio líquido deve ser aquecida de 3 25 a 375K ao ser passada em um tubo com 2 5m m de diâmetro, cuja superfície é mantida a 4 0 0K . Calcule o comprimento de tubo ne
Refrigerante-134a é transportado a 0 , 08k g / s através de um tubo de Teflon com diâmetro internoD i =2 0m m e diâmetro externo D e=2 5m m , enquanto ar atmosférico a V=28m / s e 300K escoa em escoam
NaK (45%/55%), que é uma liga de sódio e potássio, é usada para resfriar reatores nucleares de nêutrons rápidos. O NaK escoa a uma vazão de 0,8k g / s através de um tubo com diâmetro D=40m m , que tem
Para as condições do Problema 8.70, qual deve ser o comprimento da região anular se a vazão da água for de 0,35k g / s ao invés dos 0,02k g / s ?