Considere o desenvolvimento de uma camada-limite térmica laminar próxima a entrada do tubo mostrado na Figura 8.4. Quando a camada-limite fluidodinâmica é fina em relação ao diâmetro do tubo, a região de escoamento invíscico tem uma velocidade uniforme que é aproximadamente igual à velocidade média . Assim, o desenvolvimento da camada-limite é similar ao que ocorre em uma placa plana.
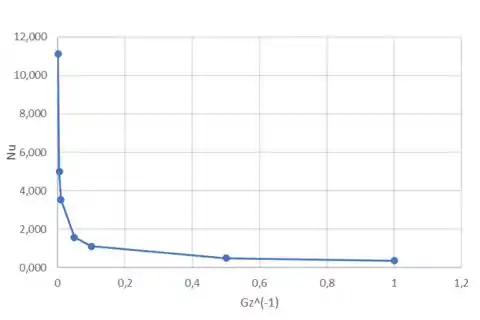
(a) Partindo da Equação 7.23, deduza uma expressão para o número de Nusselt local, NuD, como uma função do número de Prandtl, , e do inverso do número de Graetz, . Represente graficamente a expressão usando as coordenadas mostradas na Figura 8.10a, para . (b) Partindo da Equação 7.30, deduza uma expressão para o número de Nusselt médio, como uma função do número de Prandtl, , e do inverso do número de Graetz,. Compare os seus resultados com o número de Nusselt para comprimento de entrada combinada no limite de pequenos x.
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
a) Primeiro vamos escrever a Equação 7.23
Vamos transformar em , multiplicando ambos os lados por
Lembrando:
Então:
Agora vamos brincar um pouco com a matemática:
Substituindo:
Vamos dar uma ajeitadinha?
A gente sabe que:
Vamos aplicar:
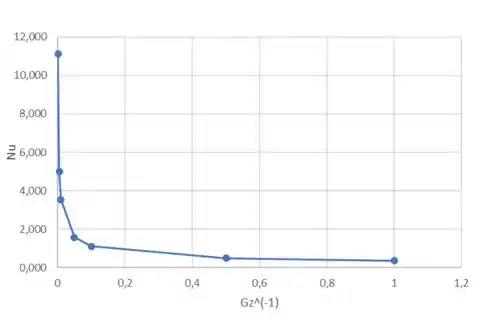
Agora temos que expressar graficamente os valores de , onde varia de 0,001 até 1 (Valor de retiradados da Figura 8,10).
Passo 2
b) Primeiro vamos escrever a Equação 7.23
Vamos transformar em , multiplicando ambos os lados por
Lembrando:
Então:
Agora vamos brincar um pouco com a matemática:
Substituindo:
Vamos dar uma ajeitadinha?
A gente sabe que:
Vamos aplicar:
Agora vamos temos:
Podemos observar que quando é muito pequeno também será, e que
Lembrando que quando
Vamos assumir que
Foi divertido!!!!
Bora matar mais uma!
Resposta