Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 123

Considere o escoamento de um gás com massa específica ρ e vazão m ˙ através de um tubo cuja superfície interna está coberta por um líquido ou um sólido sublimável com concentração mássica de vapor uniforme ρ A , s . Deduza a Equação 8.86 para a variação da concentração mássica do vapor média ρ A , μ com a distância x a partir da entrada do tubo e a Equação 8.83 para a taxa total de transferência de vapor em um tubo com comprimento L.

Passo 1

Bom, precisamos deduzir duas equações dadas no livro. Começaremos pela equação 8.86.

Para isto, vamos fazer as hipóteses iniciais que regem todo o nosso problema. Elas são: estamos em regime permanente, não há geração/consumo de massa dentro do tubo, o tubo possui perímetro P uniforme, a vazão é constante e independe da posição x .

Bom, se queremos obter uma equação, vamos precisar partir de uma análise diferencial. Para isto, ajuda fazermos um simples diagrama de um volume de controle, definindo quais os termos que “entram” no volume e quais que “saem”.

Então, temos o seguinte esboço:

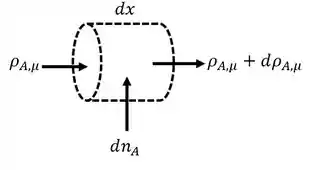
Bom, o que temos ai em cima é: na seção transversal, entra uma vazão mássica de ρ A , μ u m A c , e sai uma vazão mássica de ρ A , μ + d ρ A , μ u m A c . Notem quem temos vazão constante, por isto não diferenciamos a relação velocidade x área transversal da entrada e da saída.

Só que nós não temos apenas este termo. Temos um termo d n A “entrando” no volume de controle também. Este termo é devido a diferença entre o líquido ou sólido com densidade ρ A , s pelo gás ρ A , μ que sai pela superfície lateral. Portanto, podemos descrever este termo da seguinte forma:

d n A = h m ρ A , s - ρ A , μ d A

d n A = h m ρ A , s - ρ A , μ P d x

Passo 2

Agora que discutimos todos os termos que estarão no nosso balanço de massa, vamos fazê-lo então! Sendo assim, se a massa que entra é igual a massa que sai, temos:

ρ A , μ u m A c + ρ A , s - ρ A , μ P d x = h m ρ A , μ + d ρ A , μ u m A c

ρ A , s - ρ A , μ P d x = h m d ρ A , μ u m A c

Na equação que estamos buscando aparece o termo m ˙ . Então, vamos fazer ele aparecer ai em cima. Para isto, basta lembrar que:

m ˙ ρ = u m A c

Então,

ρ A , s - ρ A , μ P d x = h m d ρ A , μ m ˙ ρ

Se separarmos os termos diferenciais, temos:

d ρ A , μ ρ A , s - ρ A , μ = h m ρ P m ˙ d x

Agora, só nos resta integrarmos a equação diferencial acima. Se integrarmos do ponto inicial ( x = 0 e ρ A , μ = ρ A , μ , e n t ) até o ponto final ( x = x e ρ A , μ = ρ A , μ x ) , teremos:

∫ ρ A , μ , e n t ρ A , μ x d ρ A , μ ρ A , s - ρ A , μ = ∫ 0 x h m ρ P m ˙ d x

∫ ρ A , μ , e n t ρ A , μ x d ρ A , μ ρ A , s - ρ A , μ = ρ P m ˙ ∫ 0 x h m d x

- ln ⁡ ρ A , s - ρ A , μ ρ A , μ , e n t ρ A , μ x = ρ P m ˙ h - m x

ln ⁡ ρ A , s - ρ A , μ x ρ A , s - ρ A , μ , e n t = - h - m ρ P m ˙ x

Para tornarmos exatamente igual a Equação 8.86, basta aplicar a função exponencial em ambos os membros. Com isto, obtemos:

ρ A , s - ρ A , μ x ρ A , s - ρ A , μ , e n t = e - h - m ρ P m ˙ x

E assim deduzimos a primeira relação da questão!

Passo 3

Agora, vamos deduzir a segunda relação, que é a Equação 8.83. Para isto, vamos utilizar a relação que desenvolvemos anteriormente e a seguinte relação para a taxa total de transferência de vapor n A :

n A = m ˙ ρ ρ A , s a i - ρ A , e n t

Só que:

n A = m ˙ ρ ρ A , s a i - ρ A , e n t = m ˙ ρ ρ A , s a i - ρ A , e n t + ρ A , s - ρ A , s

n A = m ˙ ρ ρ A , s a i - ρ A , s + ρ A , s - ρ A , e n t = m ˙ ρ - ρ A , s - ρ A , s a i + ρ A , s - ρ A , e n t

n A = m ˙ ρ - Δ ρ A , s a i + Δ ρ A , e n t

n A = - m ˙ ρ Δ ρ A , s a i - Δ ρ A , e n t

É importante fazermos esta mudança para visualizarmos a correlação com a equação que já deduzimos anteriormente. Só que agora vamos utilizar ela quando x = L . Relembrando, temos:

ln ⁡ ρ A , s - ρ A , μ x ρ A , s - ρ A , μ , e n t = - h - m ρ P m ˙ x

ln ⁡ ρ A , s - ρ A , μ , s a i ρ A , s - ρ A , μ , e n t = - h - m ρ P m ˙ L

Reorganizando, temos:

ln ⁡ Δ ρ A , s a i Δ ρ A , e n t = - ρ m ˙ h - m P L

- m ˙ ρ = h - m P L ln ⁡ Δ ρ A , s a i Δ ρ A , e n t

Substituindo esta relação na relação de n A , temos:

n A = h - m P L Δ ρ A , s a i - Δ ρ A , e n t ln ⁡ Δ ρ A , s a i Δ ρ A , e n t

n A = h - m A s Δ ρ A , m l

E assim deduzimos a nossa segunda relação.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

124. Benzeno, um conhecido composto cancerígeno, foi derramado sobre o chão do laboratório e se espalhou por um comprimento de 2 m. Havendo a formação de uma película com 1 mm de espessura, quanto tem
129. Em um processo de secagem de papel, o papel se move sobre uma esteira transportadora a 0,2 m/s, enquanto ar seco oriundo de uma série de jatos circulares (Figura 7.18b) colide em direção normal à
127. A água de resfriamento para os condensadores de uma usina de potência é armazenada em uma lagoa de resfriamento com 1000 m de comprimento por 500 m de largura. Entretanto, devido às perdas por ev
137. Foi sugerido que a transferência de calor em uma superfície pode ser aumentada pelo seu umedecimento com água. Como um exemplo específico, considere um tubo horizontal que se encontra exposto a u
134. Ar seco, a 35°C e a uma velocidade de 15 m/s, escoa sobre um longo cilindro com 20 mm de diâmetro. O cilindro é coberto por um fino revestimento poroso que se encontra saturado com água e um aque