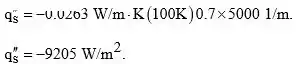Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 3
Em uma aplicação específica que envolve o escoamento de ar sobre uma superfície aquecida, a distribuição de temperaturas na camada-limite pode ser aproximada por
sendo y a distância normal à superfície e o número de Prandtl, , uma propriedade adimensional do fluido. Com , e , qual é o fluxo térmico na superfície?
Passo 1
Vamos lá gente!! Aplicando a lei de Fourier a y = 0, o fluxo de calor é,
Passo 2
Aplicando os valores que a questçao nos dá:
Resposta
Exercícios de Livros Relacionados
21. Considerando um número de Reynolds de transição igual a 5 × 105, determine a distância da aresta frontal de uma placa plana na qual a transição irá ocorrer, para cada um dos seguintes fluidos, par
Para o escoamento laminar sobre uma placa plana, sabe-se que o coeficiente de transferência de calor local hx varia com x−1/2, sendo x a distância da aresta frontal da placa (x = 0). Qual é a razão en
Para a situação descrita no Exemplo 6.4, a camada-limite pode ser levada ao estado turbulento pela aplicação de rugosidades na superfície da placa plana em uma posição específica x. Desta maneira, o l
Com uma boa aproximação, a viscosidade dinâmica μ, a condutividade térmica k e o calor específico cp são independentes da pressão. De que forma a viscosidade cinemática v e a difusividade térmica α de
Para um processo de fervura, como mostrado na Figura 1.5c, a temperatura ambiente T ∞ na lei de resfriamento de Newton é substituída pela temperatura de saturação do fluido T s a t . Considere uma sit