Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 152
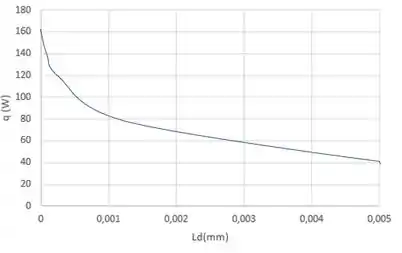
Seja o projeto B do Problema 3.151. Com o tempo, pode haver a deposição de poeira nas pequenas fendas que separam as aletas. Considere a formação de uma camada de poeira de espessura , como mostrado no desenho. Calcule e represente graficamente a taxa de transferência de calor total para o projeto B para camadas de poeira na faixa de . A condutividade térmica da poeira pode ser tomada como Inclua os efeitos da convecção nas extremidades.
Passo 1
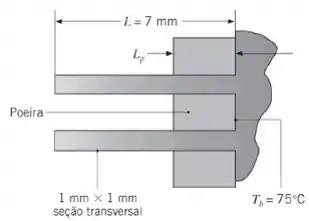
Nessa questão nós temos as dimensões de uma matriz de aletas e da camada de poeira. Além das condutividades térmicas de alumínio e poeira, temperatura da base, temperatura do ar e coeficiente de transferência de calor. Existem dois caminhos de transferência de calor, um através da poeira e no ar e outro através da aleta. Onde o circuito térmico é:
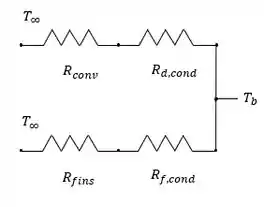
E queremos encontrar a taxa de calor permitida para a espessura da camada de poeira na faixa de .
Passo 2
Para resolver essa questão, vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A variação da temperatura através da espessura da aleta é desprezível;
(3) As propriedades são constantes;
(4) O coeficiente de transferência de calor é uniforme, inclusive nas pontas das aletas.
As resistências térmicas são dadas por:
Onde,
E,
Onde,
Sempre que tiver vamos estar nos referindo à aleta e o à poeira, beleza?
Passo 3
Onde também pode ser representado por:
E,
Finalmente, temos que:
Passo 4
Substituindo os valores nas equações acima e fazendo o cálculo para uma espessura de camada de poeira de , temos:
E,
A figura mostra a variação da taxa de calor permitida conforme a espessura da camada de poeira varia.
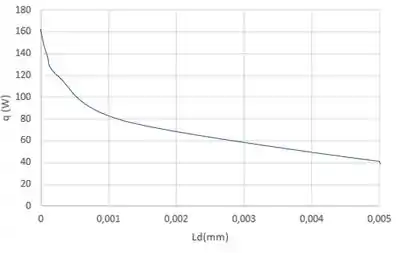
Resposta
