Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 146
Na medida em que mais e mais componentes são colocados em um único circuito integrado (chip), a quantidade de calor dissipada também aumenta. Entretanto, esse aumento está limitado pela máxima temperatura de operação permissível para o chip, que é de aproximadamente . Para maximizar a dissipação de calor, propõe-se que uma matriz de pinos de cobre seja fixada metalurgicamente à superfície externa de um chip quadrado com de lado.
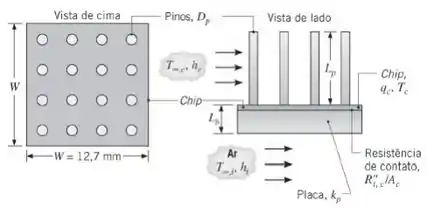
(a) Esboce o circuito térmico equivalente para o conjunto pinos-chipplaca, supondo condições unidimensionais e em regime estacionário. Despreze a resistência de contato entre os pinos e o chip. Utilizando símbolos, identifique as resistências, as temperaturas e as taxas de transferência de calor pertinentes.
(b) Para as condições especificadas no Problema 3.27, qual é a taxa máxima na qual o calor pode ser dissipado no chip, estando os pinos presentes? Isto é, qual é o valor de para ? O diâmetro e o comprimento dos pinos são e , respectivamente.
Passo 1
Aqui nós temos a geometria e resfriamento para um arranjo de placas de circuitos com chip. No qual o circuito térmico, já adiantando a letra (a), pode ser representado por:
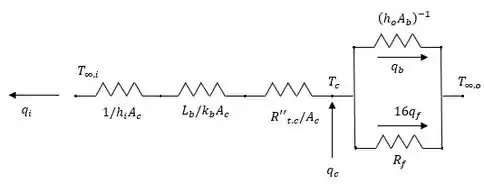
E a partir disso queremos encontrar o circuito térmico equivalente e a taxa máxima de aquecimento do chip, beleza? Então vamos lá!
Passo 2
Para resolver essa questão vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A transferência de calor é unidimensional no conjunto do chip;
(3) A resistência de contato é insignificante no chip;
(4) As propriedades são constantes;
(5) A resistência térmica é desprezível;
(6) A temperatura do chip é uniforme.
Na letra (a), além do esboço do circuito que fizemos no Passo 1, temos que:
Passo 3
Na letra (b) queremos saber qual é a taxa máxima de calor dissipado. Que pode ser escrito como:
Avaliando os parâmetros, temos:
Onde o valor de foi retirado da Tabela A.1 (Cobre à ), e:
Passo 4
Já com os parâmetros calculado, podemos analisar a taxa de calor da aleta:
A taxa de calor do topo do chip por convecção é:
A taxa de calor por convecção da placa é:
Então, a taxa máxima de calor do chip é:
Resposta
(a)
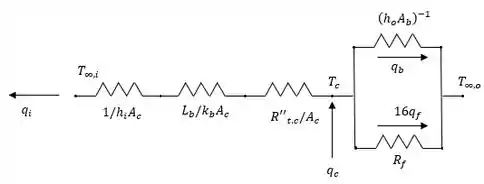
(b)