80 - Seja o tubo de vapor d’água do Exemplo 1.2. O gestor de utilidades quer uma recomendação sua sobre métodos para reduzir a perda térmica para a sala e propõe duas opções. A primeira opção restringiria a movimentação do ar ao redor da superfície externa do tubo e, assim, reduziria o coeficiente convectivo por um fator dois. A segunda opção cobriria a superfície externa do tubo com uma tinta de baixa emissividade .
(a) Quais das opções propostas você recomendaria?
(b) Para preparar uma apresentação de sua recomendação para o gestor, gere um gráfico da perda térmica como uma função do coeficiente convectivo para e emissividades de . Comente sobre a eficácia relativa da redução das perdas térmicas associadas à convecção e à radiação.
Passo 1
a)
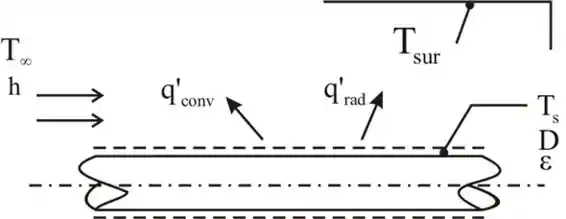
Considere a figura a seguir, mostrando o problema do exemplo 1.2 do tubo de vapor:
Passo 2
Escreva a expressão para taxa de transferência de calor do tubo para a sala por unidade de comprimento da seguinte maneira:
Aqui, a constante de Stefan Boltzmann é , a emissividade é , a temperatura da superfície do tubo , a temperatura ambiente , a área da superfície do tubo retangular é , o coeficiente de transferência de calor e a temperatura ambiente .
Substituindo pelos valores fornecidos, temos:
Passo 3
Desenhe a tabela a seguir, mostrando a taxa de transferência de calor reduzida, substituindo os valores numéricos pelas duas opções.

A taxa de transferência de calor na segunda opção é menor se comparada aos dois casos restantes.
Portanto, é recomendável usar a segunda opção que está usando um tubo com baixa emissividade. Essa opção também é mais prática em comparação à redução do coeficiente de transferência de calor.
Passo 4
b)
Escreva o seguinte programa em IHT.

Gere um gráfico variando o coeficiente de transferência de calor convectivo, , de a e calcule .
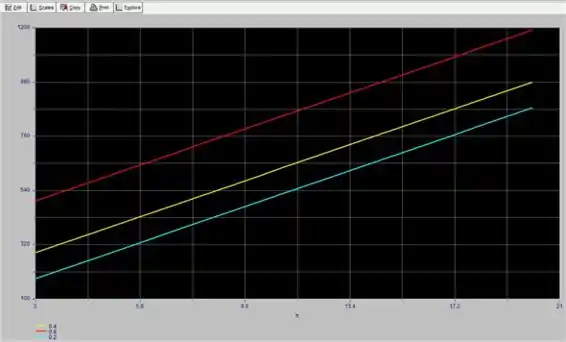
No gráfico, observe que a perda de calor é uma função do coeficiente de transferência de calor por emissividade e por convecção e observe ainda que a redução da emissividade resulta em mais redução na perda de calor.
Resposta
- Portanto, é recomendável usar a segunda opção que está usando um tubo com baixa emissividade
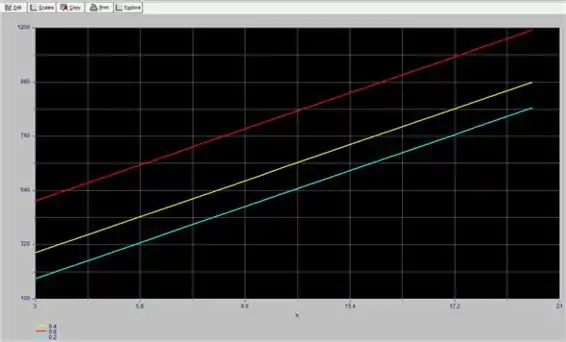
No gráfico, observe que a perda de calor é uma função do coeficiente de transferência de calor por emissividade e por convecção e observe ainda que a redução da emissividade resulta em mais redução na perda de calor.