Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 28
Uma tubulação industrial aérea de vapor d’água não isolada termicamente, com de comprimento e de diâmetro, atravessa uma construção cujas paredes e o ar ambiente estão a . Vapor pressurizado mantém uma temperatura superficial na tubulação dee o coeficiente associado à convecção natural é de A emissividade da superfície é .
(a) Qual é a taxa de perda de calor na linha de vapor?
(b) Sendo o vapor gerado em uma caldeira de fogo direto, operando com uma eficiência de ; e o gás natural cotado a por , qual é o custo anual da perda de calor na linha?
Passo 1
Essa questão nos deu o comprimento, diâmetro, temperatura da superfície e emissividade de uma linha de vapor, o coeficiente de temperatura e convecção associado ao ar ambiente e a eficiência e custo de combustível do gás queimado na caldeira. Ufa! Muita coisa né? Meio abstrato, então vamos ilustrar esse problema.
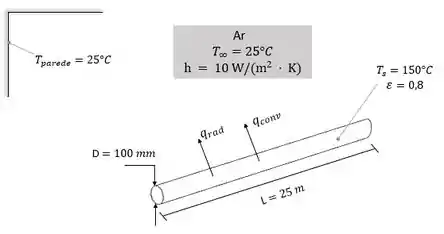
Hummmm, agora faz mais sentido o que está acontecendo e quais são nossas informações necessárias. Aqui, ele pede na letra (a), a taxa de perda de calor, e na letra (b), o custo anual da perda de calor. Então vamos resolver isso por partes.
Passo 2
Aqui, nós vamos assumir que a linha de vapor opera continuamente durante todo o ano e que a transferência líquida de radiação ocorre entre a superfície pequena (linha de vapor) e a grande (paredes da planta).
Show! Agora vamos partir para a letra (a).
Temos que na equação de perda de calor:
Onde,
Substituindo a área e os valores que temos na equação de perda de calor, ficamos com:
Passo 3
Agora vamos calcular o custo anual da perda de calor na linha, que é o que a alternativa (b) nos pede.
A perda de energia anual é:
Com um consumo de energia no forno de,
O custo anual da perda de calor é,
Com isso, nós vemos que a perda de calor e os custos relacionados são muito altos e devem ser reduzidos isolando a linha de vapor.