Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 72
72 - O teto de um carro em um estacionamento absorve um fluxo solar radiante de . A superfície inferior do teto encontra-se isolada termicamente. O coeficiente de transferência de calor por convecção entre o teto do carro e o ar ambiente é de .
(a) Desprezando a troca térmica por radiação com a vizinhança, calcule a
temperatura do teto em condições de regime estacionário se a
temperatura do ar ambiente for de .
(b) Para a mesma temperatura do ar ambiente, calcule a temperatura do teto
para uma emissividade de sua superfície igual a 0,8.
(c) O coeficiente de transferência de calor por convecção depende das
condições do escoamento do ar sobre o teto do carro, aumentando com o
aumento da velocidade do ar. Calcule e represente graficamente a
temperatura do teto em função do valor de para .
Passo 1
a)
Aplique o balanço energético e iguale a energia fornecida pelo fluxo radiante solar à energia perdida pelo telhado em convecção.
Aqui está a temperatura da superfície do telhado é , o fluxo solar radiante é , a área de superfície do telhado é , o coeficiente de transferência de calor por convecção é e a temperatura do ar ambiente é .
Agora substituindo pelos valores conhecidos, temos:
Assim, a temperatura da superfície do telhado é .
Passo 2
b)
Aplique o balanço energético e iguale a energia fornecida pelo fluxo radiante solar à energia perdida pelo telhado na convecção e na radiação.
Aqui, a constante de Stephan Boltzmann é , e a emissividade é .
Substituindo pelos valores conhecidos, temos:
Assim, a temperatura da superfície do telhado é .
Passo 3
c) Após ter calculado no computador, clique na guia 'Gráfico' e defina 'T_s' como 'Variável no eixo y' e 'h' como 'Variável no eixo x' e clique em 'OK' para gerar o seguinte gráfico.
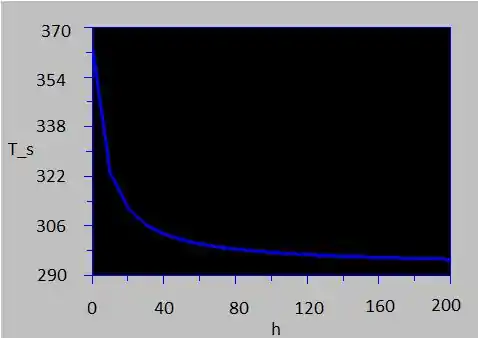
Este gráfico mostra que a temperatura da superfície diminui drasticamente com o aumento do coeficiente de transferência de calor por convecção.
