Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 72

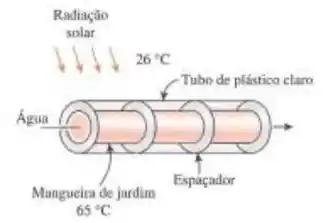
Um simples coletor solar simples é construído com a colocação de um tubo de plástico transparente de 5 cm de diâmetro em torno de uma mangueira de jardim cujo diâmetro externo é de 1,6 cm. A mangueira é pintada de preto para maximizar a absorção solar, e alguns anéis de plástico são usados para manter o espaçamento constante entre a mangueira e a cobertura plástica. Durante um dia claro, a temperatura da mangueira é medida em 65°C, enquanto a temperatura do ar ambiente é 26°C. Determine a taxa de perda de calor por convecção natural a partir da água na mangueira por metro de comprimento. Além disso, discuta como o desempenho desse coletor solar pode ser melhorado.

Passo 1

E vamos continuando as questões por aqui !!

O que nós queremos é a taxa de transferencia de calor por convecção, certo?

Mas ela pode ser calculada de duas formas:

Q c o n v ˙ = h A s T 2 - T ∞

Q c i l i n d r o ˙ = 2 π k e f f l n   D 0 D i T i - T 2

Como não temos T 1 nossa saida é consegui achar ele antes.

E para isso nós temos que lembrar que a taxa de calor transferido deve ser igual, para qualquer um dos calculos:

h A s T 2 - T ∞ = 2 π k e f f l n   D o D i T i - T 2

Como a superfície é cilíndrica:

A s = π D 0 L

Então:

π h D 0 L T 2 - T ∞ = 2 π k e f f l n   D o D i T i - T 2

O que nós sabemos?

Sabemos que:

D i = 1,6   c m = 0,016   m  

D 0 = 5   c m = 0,05   m

L = 1   m

T i = 65 ° C

T ∞ = 26 ° C

Então nós precisamos achar o coeficiente de calor convectivo e a condutividade térmica efetiva, certo?

Passo 2

A condutividade térmica efetiva é dado por:

k e f f = 0,386 k P r 0,861 + P r 0,25 F c i l i n d r i c o R a 0,25

Antes de qualquer coisa, o que fazemos?

Acertou quem disse achar a temperatura médiaaa!!

Como estamos analisando a transferência de calor através do espaçamento do cilindro, vamos usar a temperatura de 65°C, ok?

Como não temos T 2 vamos assumir que ela seja 35° para que a gente dê continuidade aos cálculos:

T m é d i a = T 1 + T 2 2 = 65 ° C + 35 ° C 2 = 5 0 ° C

Com isso nós já achamos o coeficiente de expansão volumétrica, né?

β = 1 T m é d i a = 1 5 0 + 273   K

β = 0,003 096   K - 1

Olhando na Tabela A-15 à 50°C:

k = 0,02 735   W m K

P r = 0,72 28

v T m é d i a = 1,798   × 10 - 5 m 2 s

Com isso nós achamos a condutividade térmica, mas nada sobre o número de Nusselt, né?

Para calculá-lo vamos precisar do número Rayleigh, dado por:

R a = g β T 1 - T 2 L ³ v 2 P r

Substituindo:

R a = 9,81 m s 2 0,003096   K - 1 65 ° C - 35 ° C 0,0 17   m 3 1,798     × 10 - 5 m 2 s 2 0,72 28

R a = 10008,6

Passo 3

Achamos um dado mas ainda falta o fator geométrico!!

No caso dos cilindros:

F c i l i n d r i c o = ln ⁡ D 0 D i 4 L c 3 D i - 3 5 + D 0 - 3 5 5

Sabemos que o comprimento nestes casos é dado por:

L c = D 0 - D i 2 = 0,05   m - 0,016   m 2 = 0,017   m

Substituindo:

F c i l i n d r i c o = ln ⁡ 0,05   m 0,016   m 4 0,017   m 3 0,016   m - 3 5 + 0,05   m - 3 5 5

F c i l i n d r i c o = 0,1821

Agooora sim:

k e f f = 0,386 0,02735   W m K 0,7228 0,861 + 0,7228 0,25 0,1821 × 10008,6 0,25

k e f f = 0,0567 W m ° C

Passo 4

Bom galera, para o coeficiente convectivo já sabemos que:

h = k N u L c

Como agora estamos trabalhando com a temperatura T 2 e a temperatura ambiente:

T m é d i a = T ∞ + T 2 2 = 26 ° C + 35 ° C 2 = 30,5 ° C

Com isso nós já achamos o coeficiente de expansão volumétrica, né?

β = 1 T m é d i a = 1 30,5 + 273   K

β = 0,0032948   K - 1

Para achar as propriedades nesta temperatura nós vamos ter que fazer a interpolação:

k T m é d i a = k T 1 + k T 2 - k T 1 T 2 - T 1 T m é d i a - T 1

P r T m é d i a = P r T 1 + P r T 2 - P r T 1 T 2 - T 1 T m é d i a - T 1

v T m é d i a = v T 1 + v T 2 - v T 1 T 2 - T 1 T m é d i a - T 1

Olhando na Tabela A-15:

T 1 = 30 ° C

T 2 = 35 ° C

k T 1 = 0,02588 W m K

k T 2 = 0,02625 W m K

P r T 1 = 0,7282

P r T 2 = 0,7268

v T 1 = 1,608 × 10 - 5 m 2 s

v T 2 = 1,655 × 10 - 5 m 2 s

Substituindo:

k T m é d i a = 0,02588 W m K + 0,02625 - 0,02588 W m K 35 ° C - 30 ° C 30,5 ° C - 30 ° C = 0,025917   W m K

P r T m é d i a = 0,7282 + 0,7268 - 0,7282 35 ° C - 30 ° C 30,5 ° C - 30 ° C = 0,72806

v T m é d i a = 1,608 × 10 - 5 m 2 s + 1,655 × 10 - 5 - 1,608 × 10 - 5 m 2 s 35 ° C - 30 ° C 30,5 ° C - 30 ° C = 1,6127   × 10 - 5 m 2 s

Com isso tudo nós já conseguimos calcular o número de Rayleigh:

R a = g β T 1 - T 2 L c ³ v 2 P r

Lembrando que neste caso:

L c = D 0 = 0,05   m

Substituindo:

R a = 9,81 m s 2 0,0032948   K - 1 35 ° C - 26 ° C 0,05   m 3 1,6127       × 10 - 5 m 2 s 2 0,72806

R a = 1,0179 × 10 5

Para um cilindro na horizontal:

N u = 0,6 + 0,387 . R a 1 6 1 + 0,559 P r 9 16 8 27 2

Substituindo:

N u = 0,6 + 0,387 . 1,0179 × 10 5 1 6 1 + 0,559 0,72806 9 16 8 27 2

N u = 7,8377

Bora calcular o coeficiente convectivo?

h = 0,025917   W m ° C × 7,8377 0,05   m

h = 4,0626   W m ² ° C

Passo 5

E depois de tantos cálculos, se lembram o que fazer ?

Colocar na igualdade, né ?!

Então bora lá:

π 4,0626   W m 2 K 0,05   m 1   m T 2 - 26 ° C = 2 π 0,0567 W m ° C l n   0,05   m 0,016   m 65 ° C - T 2

0,63812   T 2 - 26 ° C = ( 0 , 3127 ) 65 ° C - T 2

T 2 = 38,82 ° C

Bem próximo do que estipulamos, não é?

Então podemos dar sequencia e substituir esta temperatura em uma das equações:

Q c o n v ˙ = 0,63812 W ° C 38,82 ° C - 26 ° C

Q c o n v ˙ = 8,18   W

Cansaram?

Força guerreiros, nós ainda temos muitas questões pela frente !!

Resposta

Q c o n v ˙ = 8,18   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

90 – Uma folha de papel molhado de 205mm x 245mm está pendurado em um dia quente e ensolarado. O ar ainda está na temperatura de 30°C e a umidade relativa é de 40%. Para maximizar a taxa de secagem, a
77 – Esboce o gráfico da perda de calor por unidade de comprimento do coletor solar do problema 9.76 sobre uma faixa de 0,1 ≤ D0 ≤ 0,25 m assumindo (i) transferência de calor por condução através do e
Refaça o exemplo 9.4 , admitindo a existência do escoamento de ar seco a uma velocidade de:a) v ∞ = 0,1m / s ;b) v ∞ = 0,1m / h ;c) v ∞ = 10m / s ;d) v ∞ = 100m / s .
Avalie a necessidade de considerar a presença da convecção mássica natural no exemplo 8.10 .
Calcule o coeficiente convectivo médio natural de transferência de massa para uma esfera de naftaleno de 3c m de diâmetro, mantida em um ambiente a 60° Ce 1 a t m .