Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 9.Problemas - Ex. 77
77 – Esboce o gráfico da perda de calor por unidade de comprimento do coletor solar do problema 9.76 sobre uma faixa de 0,1 ≤ D0 ≤ 0,25 m assumindo (i) transferência de calor por condução através do espaço anular (ii) transferência de calor por convecção através do espaço anular. Determine o diâmetro externo que forneça a mínima perda de calor através do espaço de ar por unidade de comprimento do coletor, e o valor desta perda.
Passo 1
A taxa de transferência de calor por unidade de comprimento pelo problema 9.76 vai ser a seguinte, considerando uma condução de calor através do ar no espaço anular entre os cilindros
Onde,
-q’ é a taxa de transferência de calor por unidade de comprimento;
-L é o comprimento;
-kef é a condutividade térmica efetiva;
-Ti é a temperatura interna;
-To é a temperatura externa;
-Di é o diâmetro interno;
-Do é o diâmetro externo;
Vamos pegar os dados do problema 9.76 que serão uteis para os cálculos:
Os dados do problema 9.76 são:
Para o ar a 330K, pela Tabela A.4:
Passo 2
A condutividade térmica efetiva pode ser determinada pela seguinte expressão
Onde para Rayleigh (Rac):
Onde LC para tubos cilíndricos concêntrico é calculado pela expressão abaixo:
Assim para Rayleigh:
Passo 3
Vamos deixar Rayleigh em função apenas de Do:
Substituindo os valores, exceto para Do
Fazendo a mesma coisa para kef, que vai ficar em função de Rayleigh
E para q’
Substituindo o kef para q’ ficar em função apenas de Rayleigh:
Assim, para você plotar o gráfico, para os valores de Do, calcule Rayleigh para cada Do e depois calcule o q’, com o valore de Do e o Rayleigh correspondente.
Passo 4
Para realizar tal tarefa, usar uma ferramenta gráfica é a melhor opção, pois vai te economizar tempo por ser mais prático.
Usando o EXCEL, para obter os dados de q’ vs Do e plotar o gráfico:
Obteve-se os seguintes dados:
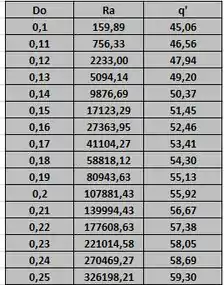
Com os dados acima, obteve-se o seguinte gráfico:
Pelo gráfico vemos que o valor de Do que minimiza q’ é
O valor mínimo de q’ é então:
Resposta
