Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 115
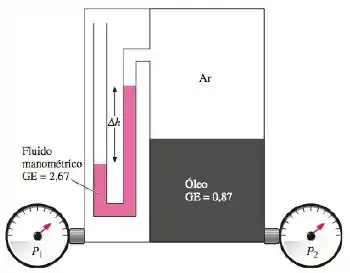
Um sistema está equipado com dois medidores de pressão e um manômetro, como mostra a figura . Para , determina a diferença de pressão .
Passo 1
Devido a diferença de coluna de fluido manométrico a diferença de pressão entre há de ser determinado.
Assumindo que todos os fluidos são incompressíveis e o efeito da coluna de ar é insignificante.
Temos a seguintes propriedades a gravidade específica do ao fluido manométrico de e para o óleo e tomaremos a densidade padrão da água .
Tendo estes itens explanados, temos que para resolver está questão iremos começar com a pressão indicada , e iremos movendo ao longo dos tubos (somando as pressões assim como vamos “andado” para baixo), diminuindo a pressão (assim como vamos para cima nos tubos) até chegar em .
Assumirei a notação de para o fluido manométrico.
Passo 2
Seguindo oque foi explicado no passo 1, temos:
Como desejamos a diferença e rearranjando a equação pelos termos em comum, temos:
Substituindo os valores temos:
Pressão se mostra negativa devido a pressão no óleo é maior do que a que se passa no fluido manométrico.
Resposta
Pressão se mostra negativa devido a pressão no óleo é maior do que a que se passa no fluido manométrico.