Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 58
Nutrientes dissolvidos em água são levados para as partes superiores das plantas através de tubos pequenos devido em parte ao efeito capilar. Determine a altura que a solução subirá numa árvore num tubo de diâmetro como resultado do efeito capilar. Trate a solução como água a com ângulo de contato de .
Passo 1
Por mais que a questão fale sobre nutrientes subindo através de árvores, podemos aproximar esse transporte de nutriente como se fosse a elevação do nível da água dentro de um tubo fino por causa do efeito capilar. Com essa aproximação, podemos calcular a altura que a solução de nutrientes subirá com a equação do livro.
é o ângulo de contato entre a reta tangente à superfície do líquido e a superfície do tubo.
é a tensão superficial do líquido (água). é o raio do tubo. é a aceleração da gravidade. é a densidade da água.
Passo 2
Para simplificar a nossa vida, vamos ilustrar os dados informados pelo enunciado através da figura abaixo.
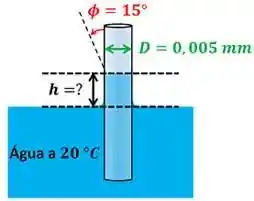
No próximo passo vamos expor e converter as unidades de todos os dados que o enunciado informou.
Passo 3
O enunciado nos informou o valor de todas as variáveis que precisamos.
Nos exercícios, a densidade da água a geralmente vale:
Além disso, a tensão superficial da água a se encontra na tabela do livro.
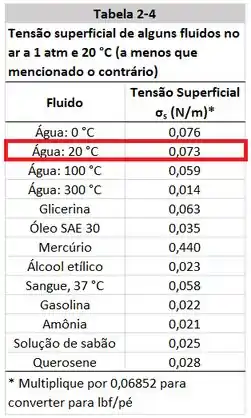
No próximo passo nós vamos iniciar as contas.