Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 113

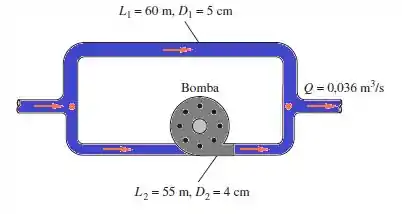
O sistema de tubos de aço galvanizado em paralelo da figura abaixo fornece água a 20°C com uma vazão total de 0, 036 m³/s. Se a bomba está totalmente aberta, mas desligada, com um coeficiente de perda de K = 1,5 , determine (a) a vazão em cada tubo e (b) a queda total de pressão.

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.

ρ = 998   k g / m ³

μ = 0,001   k g / m . s

Bem, os tubos são feitos de aço galvanizado, ou seja, todos eles devem possuir a mesma rugosidade ϵ = 0,15   m m , portanto a rugosidade relativa é:

Passo 2

Vamos começar assumindo que nosso escoamento é turbulento e que temos a mesma queda de pressão em cada uma das ramificações, essas quedas de pressão serão causadas pelas perdas de carga maiores na ramificação superior e na de baixo temos as perdas localizadas e maiores.

h f 1 = f 1 L 1 D 1 V 1 2 2 g

h f 2 + h m 2 = f 2 L 2 D 2 V 2 2 2 g + V 2 2 2 g K = V 2 2 2 g f 2 L 2 D 2 + K

Também pelo balanço de massa, a gente vai ter que a vazão total de saída deve ser igual a vazão que está saindo pela ramificação superior somada a vazão que está saindo na ramificação inferior.

Q 1 + Q 2 = V 1 π 4 D 1 2 + V 2 π 4 D 2 2 = 0,036   m 3 / s

Passo 3

(a) Note que vamos precisar chutar um valor do fator de atrito porque ele depende de Reynold que depende da velocidade que não temos ainda como calcular. Então você já pode ficar preparado porque toda vez que a gente “chutar” f, provavelmente vamos recair num cálculo iterativo.

Vamos chutar f = 0,02

Vimos que h f 1 = h f 2 + h m 2

f 1 L 1 D 1 V 1 2 2 g = V 2 2 2 g f 2 L 2 D 2 + K

0,02 60 0,05 V 1 2 2 9,81 = V 2 2 2 9,81 + 0,02 55 0,04 + 1,5 → V 1 = 1,1 V 2

Passo 4

Opa!!! Achamos uma relação entre V1 e V2, isso quer dizer que podemos pegar nossa equação do balanço de massa e substituir V1, certo?

π 4 0,05 2 1,1 V 2 + π 4 0,04 2 V 2 = 0,036 → V 2 = 10,54 m s

E aí temos que V 1 = 11,6   m / s

Olha que beleza então, encontramos agora os valores de V1 e V2, e podemos calcular seus respectivos Reynolds e encontrar o novo valor de fator de atrito para cada um desses Re e rugosidade relativa.

Passo 5

Fazendo isso, encontramos pro primeiro chute que

R e 1 = 578000   ,   f 1 = 0,0264

R e 2 = 421000 ,   f 2 = 0,0282

Com isso seguimos nosso algoritmo de iteração!!! Fazemos esse processo até a convergência dos valores de V1 e V2.

  1. Chutar f 1 = f 2 = f
  2. Calcular a relação V1 e V2
  3. Substituir no balanço de massa
  4. Achar V1 e V2
  5. Calcular Reynold
  6. Achar os novos valores de f 1 e f 2
  7. Voltar ao passo (2) até convergência nos valores de V1 e V2

Esse processo você pode montar em algum software qualquer ou ir fazendo na mão mesmo só pra você pegar a ideia da parada, sacou?!

Ao final, você vai observar que os valores convergem pra em torno de:

f 1 = 0,0264   ,   V 1 = 11,7   m / s

f 2 = 0,0282   ,   V 2 = 10,4   m / s

Com isso, podemos agora finalmente calcular os valores de vazão de cada um dos tubos!!!

Q 1 = A 1 V 1 = π 4 D 1 2 V 1 = 0,023   m 3 / s

Q 2 = A 2 V 2 = π 4 D 2 2 V 2 = 0,013   m 3 / s

Passo 6

(b) A queda de pressão será da pela igualdade feita nos passos anteriores com as perdas de carga!!

Δ p = f 1   L 1 D 1 ρ V 1 2 2 = f 2 L 2 D 2 + 1,5 ρ V 2 2 2 = 2,16   x   10 6   P a

Resposta

  1. Q 1 = A 1 V 1 = π 4 D 1 2 V 1 = 0,023 m 3 s             Q 2 = A 2 V 2 = π 4 D 2 2 V 2 = 0,013   m 3 / s
  2. Δ p = 2,16   x   10 6 P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o princípio operacional dos medidores de vazão de área variável (rotâmetros)? Como eles se comparam aos outros tipos de medidor de vazão com relação ao custo, perda de carga e confiabilidade?
Quais são as principais considerações ao selecionar um medidor de vazão para medir a vazão de um fluido?
Qual a diferença entre os princípios operacionais dos anemômetros térmicos e laser Doppler?
Explique como a vazão é medida com medidores de vazão do tipo por obstrução. Compare os medidores de orifício, de bocais de escoamento e os medidores de Venturi com relação ao custo, tamanho, perda de
Explique como a vazão é medida com um tubo estática de Pitot e discuta suas vantagens e desvantagens com relação ao custo, queda de pressão, confiabilidade e exatidão.