Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 124

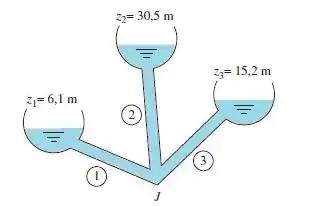
O sistema de três reservatórios da figura abaixo fornece água a 20°C. Os dados do sistema são:

D 1 = 200   m m                                               D 2 = 150   m m                                                     D 3 = 225   m m

L 1 = 549   m m                                                   L 2 = 366   m m                                                           L 3 = 488   m m        

Todos os tubos são de aço galvanizado. Calcule a vazão em todos eles.

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.

ρ = 998   k g / m ³

μ = 0,001   k g / m . s

Bem, os tubos são feitos de aço galvanizado, ou seja, todos eles devem possuir a mesma rugosidade ϵ = 0 , 1524   m m , portanto a rugosidade relativa é:

R u g o s i d a d e 1 = 0 , 1524   x 10 - 3 200   x   10 - 3 = 0,00 0762

R u g o s i d a d e 2 = 0,1524   x 10 - 3 15 0   x   10 - 3 = 0,00 102

R u g o s i d a d e 3 = 0,1524   x 10 - 3 2 25   x   10 - 3 = 0,0006 77

Passo 2

Vamos denotar de “a” a interseção dos tubos. Nesse ponto, a perda de carga deve ser igual para todos os tubos, certo? Você também vai concordar comigo que a perda de carga deve ser igual a altura de água subtraindo a quantidade de pressão que foi perdida pelo deslocamento do fluido naquele tubo?

z 1 - h a = f 1 L 1 D 1 V 1 2 2 g

z 2 - h a = f 2 L 2 D 2 V 2 2 2 g

z 3 - h a = f 3 L 3 D 3 V 3 2 2 g

Além disso temos a equação do balanço de massa que diz que Q 1 + Q 2 + Q 3 = 0

Passo 3

O que nós vamos fazer agora? Vamos chutar um valor de h a e depois iterar para cada valor de fator de atrito para encontrar a velocidade V e posteriormente a vazão Q e verificar que a soma das vazões deve ser igual a zero.

Chutando h a = 15 , 2   m

z 1 - h a = f 1 L 1 D 1 V 1 2 2 g

6,1 - 15 = f 1   549 200   V 1 2 2 9,81

Precisaríamos chutar um valor de f = 0,0194 e assim encontramos uma velocidade V 1 = - 1,85   m / s

Similarmente para os outros tubos chutamos f 2 = 0,0204 obtendo V 2 = 2,47   m / s , e V 3 = 0 , pois, z 3 - h a = 0 .

Isso dará Q 1 + Q 2 + Q 3 = - 0,0153   m 3 / s

Passo 4

Bem, o resultado para mim já estaria satisfatório, porém, se você tentar com um valor de h a = 14,9 , você obterá valores mais próximos de zero ainda, os quais ao final darão valores de vazão como sendo:

Q 1 = 0,64 m 3 s                                                       Q 2 = 0,49 m 3 s                                                 Q 3 = 0,15   m 3 / s

Resposta

Q 1 = 0,64 m 3 s                                                       Q 2 = 0,49 m 3 s                                                 Q 3 = 0,15   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em prédios grandes, a água quente de um tanque de água circula através de um laço, para que o usuário não tenha que esperar até que toda a água da tubulação longa drene antes que a água quente comece
A vazão da amônia a 10°C ( ρ = 624,6k g / m ³ ³ e μ = 1,697x10 - 4 k g m . s ) através de um tubo com 3 cm de diâmetro deve ser medida com um bocal de escoamento com diâmetro de 1,5 cm equipado com um
Um sistema de aquecimento distrital geotérmico envolve o transporte da água geotérmica a 110°C de um poço geotérmico para uma cidade com a mesma altitude por uma distância de 12 km, a uma vazão de 1,5
Um medidor Venturi vertical equipado com um medidor de pressão diferencial é mostrado na Figura P8-97 e usado para medir a vazão de propano líquido a 10 ° C ( ρ = 514,7k g / m ³ ³) através de um tubo
Durante um acampamento, você percebe que a água é descarregada de um reservatório alto para um riacho no vale através de um tubo de plástico de 30 cm de diâmetro. A diferença de altitude entre a super