Um resistor elétrico está conectado a uma bateria, conforme mostrado no esquema. Após um curto período em condições transientes, o resistor atinge uma temperatura de equilíbrio de, aproximadamente uniforme. A bateria e os fios condutores, por sua vez, permanecem à temperatura ambiente de. Despreze a resistência elétrica nos fios condutores.

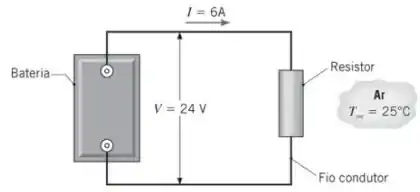
(a) Considere o resistor como um sistema ao redor do qual uma superfície de controle é posicionada e a Equação é aplicada. Determine os valores correspondentes de), e Se uma superfície de controle for colocada ao redor de todo o sistema, quais são os valores de), e ?

(b) Se energia elétrica for dissipada uniformemente no interior do resistor, que é um cilindro com diâmetro e comprimento , qual é a taxa de geração de calor volumétrica, ?

(c) Desprezando a radiação a partir do resistor, qual é o coeficiente convectivo?

Para resolver essa questão, vamos assumir que:

1. A energia elétrica é dissipada uniformemente dentro do resistor;
2. A temperatura do resistor é uniforme;
3. A energia elétrica dissipada nos fios condutores é desprezível;
4. A Troca de radiação entre o resistor e o ambiente é desprezível;
5. Não ocorre transferência de calor da bateria;
6. Estamos em condições de estado estacionário.

Ufa! Bastante coisa, mas agora podemos resolver nossa questão em paz \o/

A conservação de energia necessária para o volume de controle em um instante de tempo é:

onde correspondem aos processos de entrada e saída de superfície, respectivamente. O termo de geração de energia, está associado à conversão de alguma outra forma de energia (química, elétrica, eletromagnética ou nuclear) em energia térmica. O termo está associado a alterações na energia interna, cinética e / ou potencial da matéria no volume de controle.

são fenômenos do volume de controle. A energia elétrica fornecida pela bateria é:

Fazendo a letra (a) temos duas situações, a primeira é considerando o nosso volume de controle sendo o resistor, temos:

O termo é devido à conversão de energia elétrica em energia térmica e o termo é devido à convecção da superfície do resistor para o ar.

Na segunda situação vamos considerar o volume de controle como sendo o sistema bateria-resistor, temos:

O termo representa a diminuição da energia química dentro da bateria. A conversão de energia química em energia elétrica e sua subsequente conversão em energia térmica são processos internos ao sistema que não estão associados aou . O termo é devido à convecção da superfície do resistor para o ar.

Na letra (b), queremos calcular a taxa de geração de calor volumétrica, . Então, precisamos calcular o nosso volume:

Do balanço de energia com o resistor sendo nosso volume de controle, temos:

Substituindo os valores,

Encontramos uma taxa de geração de calor volumétrica de:

E por último, vamos à letra (c), em que queremos saber o coeficiente convectivo desprezando a radiação a partir do resistor.

Pelo balanço de energia no resistor e a Lei de Newton de resfriamento com a área superficial sendo:

Temos,