Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 37
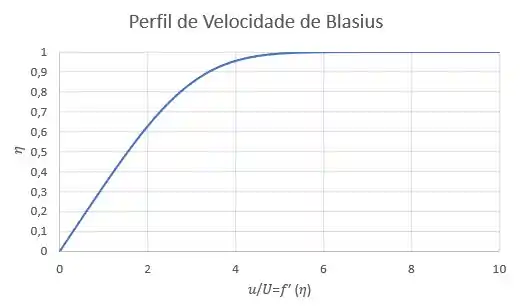
A solução exata de Blasiu envolve a resolução de uma equação não linear, Eq 9.11, com condições iniciais e de contorno dadas pela Eq 9.12. Desenvolva, em uma planilha no software Excell, um procedimento para obter uma solução numérica para este sistema de equações. A planilha deve apresentar colunas para contendo linhas com valores calculados destas três últimas para passos numéricos adequados de (por exemplo, 1000 linhas de valores de para passos de de , com variando de a para ir além dos dados da Tabela 9.1). Os valores de e para a primeira linha são iguais a zero (conforme as condições iniciais, Eq. 9.12); um valor inicial estimado é necessário para (tente 0,5). Os valores subsequentes das linhas para podem ser obtidos dos valores da linha anterior usando, por exemplo, o método de Euler de diferenças finitas da Seção 5.5 para aproximação de derivadas de primeira ordem (e a Eq 9.11). Finalmente, uma solução pode ser encontrada usando as funções do “Resolvedor Excel (Excel’s Goal Seek or Solver) para alterar o valor inicial de até que seja igual a 1 para grandes valores de (por exemplo, , condição de contorno da Eq. 9.12). Trace um gráfico dos resultados. Nota: O método de Euler é relativamente grosseiro, e seu uso levará a resultados com erros de aproximadamente .
Passo 1
Vamos reunir todas essas equações aí que ele falou:
A gente pode lembrar também que:
O enunciado quer a que a gente ache a nossa própria solução numérica para essa equação usando o método de Euler. Vamos começar!
Passo 2
Para começar, a gente vai criar as colunas e colocar os valores de entre e , com passos de .
Depois seguindo as condições de contorno, colocamos .
Por fim, vamos chutar
Aí a gente vai ter essa tabela, até agora:
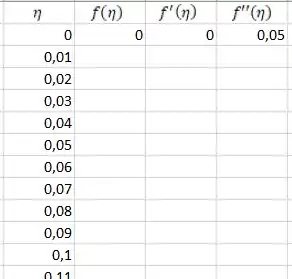
(a tabela está cortada, mas vai até 10)
Passo 3
Agora precisamos usar o método de Euler para completar a tabela. Como vai funcionar?
Ele tem essa carinha:
Mas da nossa equação diferencial, a gente tem que:
Então a gente pode escrever que:
Como , a gente vai usar essas três equações para completar a tabela a partir da primeira linha:
Nossa tabela fica assim (o comecinho dela):
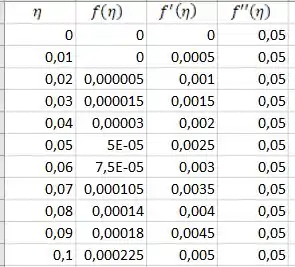
Passo 4
A gente precisa encontrar o verdadeiro valor de usando o “Resolvedor Excel”. Aí nós usamos a condição de contorno:
No nosso caso:
É só a gente dizer que quer que o valor da célula que fique igual a , variando a célula que está .
Fazendo isso, a gente fica com essa tabelinha:
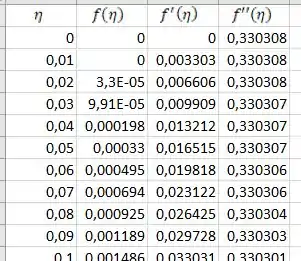
Passo 5
Agora com os dados certinhos, só gerar o gráfico:
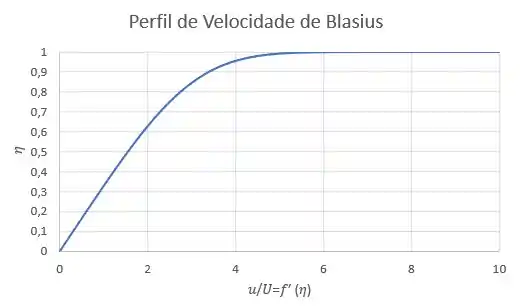
Resposta
