Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 48
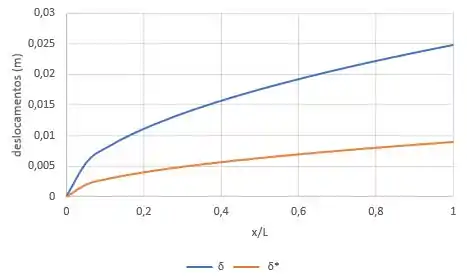
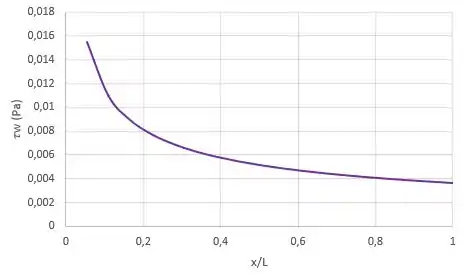
Uma superfície horizontal, de comprimento e largura , está imersa em uma corrente de ar-padrão escoando a . Considere a formação de uma camada limite laminar e aproxime o perfil de velocidade como senoidal. Trace e versus para a placa.
Passo 1
Precisamos achar uma relação entre e e para conseguir traçar o gráficos que ele pediu.
O enunciado fala que temos um perfil de velocidade senoidal:
E também dá outras informações:
- comprimento da placa:
- largura:
- velocidade de corrente livre:
- ar-padrão: e
Vamo começar!
Passo 2
Podemos usar a equação integral da quantidade de movimento:
Considerando :
E gente pode dizer que:
Sabendo que:
Substituindo isso na equação integral:
Passo 3
Aí a gente precisa lembrar que:
Separando a integral em duas, usando uma substituição simples e a identidade resolvemos a integral:
Aí substituindo na nossa equação:
Passo 4
Isso é uma equação diferencial separável, então vamos separar as variáveis e resolver:
Ih como a gente acha esse C aí? A gente pode assumir que em , .
Resolvendo esse PVI, a gente vê que
Então:
Isolando :
Achamos a primeira expressão!
Passo 5
Para achar uma expressão para vamos usar:
Mas a gente sabe quem é
Passo 6
Para finalizar, vamos achar usando sua definição:
Conseguimos!
Passo 7
Agora só montar os gráfico com as informações do enunciado e as expressões que achamos:
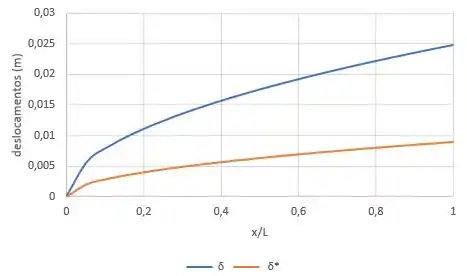
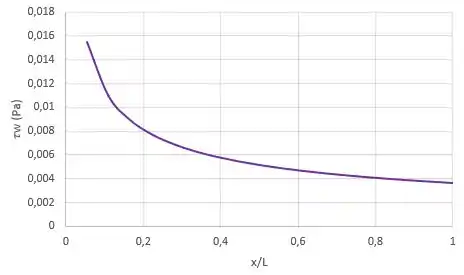
Resposta
