Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 53

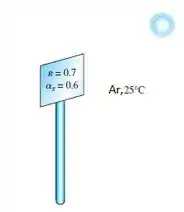
Uma superfície de uma placa de rua 0,2   m × 0,2   m tem absorvidade de 0,6 e emissividade de 0,7. A radiação solar é incidente na placa de rua a uma taxa de 200 W m 2 , e o ar ao redor é de 25°C. Determine a temperatura da superfície da placa de rua. Suponha que a temperatura da película seja 30°C.

Passo 1

Bora pra mais umaaa !!

Bom galera, existem duas formas de calor sendo transferidas para a placa, convectiva e radioativa:

Q ˙ = Q c o n v e c t i v a ˙ + Q r a d i o a t i v a ˙

Se vocês não se lembram como calculamos cada uma, eu mostro:

Q ˙ = q i n c i d e n t e A s α

Q c o n v e c t i v a ˙ = h A s T s u p - T ∞

Q r a d i o a t i v a ˙ = ε σ A s T s u p 4 - T ∞ 4

Onde q i n c i d e n t e é o calor incidente na placa por metro quadrado, A s a área da superfície, h é o coeficiente convectivo, α é a absorvidade, ε a emissividade e σ   constante de Boltzmann. Temos ainda a temperatura da superfície, T s u p , e a temperatura do ambiente, T ∞ .

Então:

q i n c i d e n t e A s α = h A s T s u p - T ∞ + ε σ A s T s u p 4 - T ∞ 4

Removendo a área dos termos:

q i n c i d e n t e α = h T s u p - T ∞ + ε σ T s u p 4 - T ∞ 4

Agora que já lembramos o que é cada um dos dados, vamos ver o que o problema nos deu:

α = 0,6

ε = 0,7

σ = 5,67 × 10 - 8 W m 2 K 4

T ∞ = 25 ° C + 273 = 298 K

q i n c i d e n t e = 200 W m 2

Belezaa!! Nem tudo são flores, já temos muitas coisas, mas ainda não temos o coeficiente de convecção.

Passo 2

E como faremos pra achar o coeficiente convectivo?

Simples!!

Basta usarmos a equação:

N u = h L k

Isolando:

h = N u k L

Sabendo que:

L = 20   c m = 0,2   m

E supondo que a temperatura do ar na película é de 30°C, como nos foi dito, e olhando na Tabela A-15:

k = 0,02588 W m K

P r = 0,7282

v = 1,608 × 10 - 5 m ² s

Com isso nós também podemos achar o coeficiente de expansão volumétrica:

β = 1 T m é d i a = 1 ( 30 + 27 3 )   K = 0,0033   K - 1

Achamos várias informações, né?

Mas ainda não temos o número de Nusselt.

Como acharemos? Para essas condições:

N u = 0,59 . R a 1 4

Se:

R a = g β T s u p - T ∞ L ³ v 2 P r

Então:

N u = 0,59 . g β T s u p - T ∞ L 3 v 2 P r 1 4

Agora é só colocar nossos dados, como nós não sabemos o valor da superfície vamos assumir que seja próximo a 35°C, ok?

Isso porque a placa esta recebendo calor, então provavelmente ela vai estar um pouco mais quente que a película de ar próxima.

Substituindo os dados:

N u = 0,59 . 9,81 m s 2 0,0033   K - 1 35 ° C - 25 ° C ( 0,2   m ) ³ 1,608 × 10 - 5 m ² s 2 × 0,7282 1 4

N u = 30,66

Passo 3

Agora nós podemos achar o coeficiente convectivo:

h = 30,66 0,02588 W m K 0,2   m

h = 3,967   W m ² K  

Agora nós achamos tudo que precisamos para calcular a temperatura da superfície:

200 W m 2 ( 0,6 ) = 3,967   W m 2 K T s u p - 298 K + ( 0,7 ) 5,67 × 10 - 8 W m 2 K 4 T s u p 4 - 298 K 4

Resolvendo a equação de grau quatro nós achamos:

T s u p = 312,155   K

Em graus Celsius:

T s u p = 312,155   K - 273 = 39,155 ° C

Então a temperatura da superfície da placa será 39,155°C, bem próximo à temperatura que assumimos anteriormente, não é?

Resposta

39,155 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar, a 3a t m e 100 ° C , é descarregado de um compressor em um receptor vertical com2,5m de altura e 0,75m de diâmetro. Suponha que a parede do receptor apresente resistência térmica desprezível, este
Seja o escoamento laminar ao longo de uma placa isotérmica vertical de comprimento L , fornecendo um coeficiente de transferência de calor médio de h - L . Se a placa for dividida em N placas menores,
Considere uma janela simples (com uma única lâmina de vidro) vertical com largura e altura iguais ( W=L=1m ) . A superfície interior está exposta ao ar e às paredes do quarto, que estão a 18 ° C . Sob
A porta de um refrigerador tem uma altura de H=1m e uma largura de W=0,65m , e está localizada em uma grande sala na qual o ar e as paredes estão a T ∞=T v i z=25 ° C . A porta é formada por uma camad
Considere um experimento para investigar a transição para o escoamento turbulento em uma camada-limite de convecção natural que se desenvolve ao longo de uma placa vertical suspensa em uma grande sala