Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 125

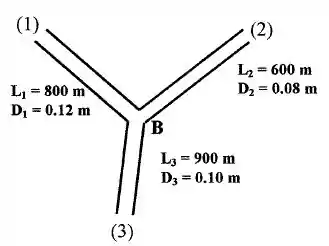
Suponha que os três tubos de ferro fundido do problema a seguir sejam conectados de modo que se encontrem suavemente no ponto B, como mostrado abaixo. As pressões de entrada 1, 2 e 3 são 200 kPa, 160 kPa e 100 kPa, respectivamente. O fluido é água a 20°C. Despreze as perdas localizadas. Calcule a vazão em cada tubo e determina se ela vai em direção ao ponto B ou em sentido contrário.

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.

ρ = 998   k g / m ³

μ = 0,001   k g / m . s

A pressão no ponto B deve ser conhecida e constante a qual deve fazer o fluxo líquido igual a zero na junção B. É claro no desenho que o fluxo vai de (1) para B e de (B) para 3, mas não sabemos exatamente sobre o tubo (2). Considerando que os tubos são feitos de aço fundido, temos ϵ = 0,26   m m .

Passo 2

Cada tubo tem sua vazão baseada na queda de pressão causada pelas perdas de carga, ou seja:

Δ p ρ g = f L D V 2 2 g

p 1 - p B = f 1 L 1 D 1 ρ V 1 2 2

p 2 - p B = f 2 L 2 D 2 ρ V 2 2 2

p B - p 3 = f 3 L 3 D 3 ρ V 3 2 2

Porém, note que estamos caindo em um problema iterativo, certo?

Passo 3

O valor de f pode ser obtido no diagrama de Moody quando se conhecemos ϵ D   e   R e . O valor correto de p B faz com que a vazão Q i = π 4 D i 2 V i balanceie nossa equação na junção B.

Podemos fazer o cálculo pensando da seguinte maneira:

  1. Chute p B = ( p 1 + p 2 + p 3 ) / 3  
  2. Chute um valor de f
  3. Encontre as velocidades
  4. Calcule Re
  5. Calcule a vazão líquida na junção e verifique se está próximo de zero o somatório destas vazões. Caso esteja, pode parar aqui! Caso não, vá para o passo seguinte.
  6. Obtenha um novo valor de f no diagrama de Moody
  7. Com a velocidade do ponto (3) e o novo valor de f, volte em (3)

Esse processo deve ser feito até que ∑ Q ≈ 0

Passo 4

Ao final do processo de convergência, você perceberá que o valor de p B convergido é de 166,7 kPa. Uma vez convergido p B , damos prosseguimento aos cálculos de f de forma iterativa até obtenção de:

f 1 = 0,0260                   R e 1 = 74300             ϵ D 1 = 0,00217                     Q 1 = 0,007   m 3 / s

f 2 = 0,0321                   R e 2 = 18900             ϵ D 1 = 0,00325                     Q 2 = - 0,0012   m 3 / s

f 3 = 0,027                   R e 3 = 7400             ϵ D 1 = 0,0026                     Q 3 = - 0,0058   m 3 / s

Resposta

Q 1 = 0,007   m 3 / s

Q 2 = - 0,0012   m 3 / s

Q 3 = - 0,0058   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água deve ser retirada de um reservatório de água com 5m de altura perfurando um orifício bem arredondado com 3c m de diâmetro com perda desprezível na superfície inferior eanexando uma curva horizont
Água a 15 ° C deve ser descarregada de um reservatório a uma taxa de 18L / s usando dois tubos de ferro fundido horizontais em série e uma bomba entre eles. O primeiro tubo tem 20m de comprimento e di
A vazão da água através de um tubo com diâmetro de 10 cm deve ser determinada medindo a velocidade da água em diversos locais ao longo de uma seção transversal. Para o conjunto de medidas dadas na tab
Um duto de seção anular de folga muito pequena provoca uma queda de pressão muito grande e é útil para uma medição precisa da viscosidade. Se um duto de seção anular liso de 1 m de comprimento, com a
Óleo SAE 10 a 20 ° C escoa a uma velocidade média de 2 m/s entre duas placas horizontais, paralelas e lisas, distantes de 3 cm. Calcule (a) a velocidade na linha de centro, (b) a perda de carga por me