Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 105

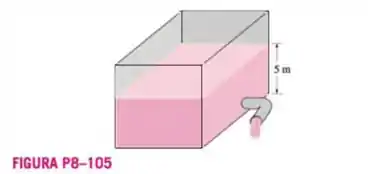
Água deve ser retirada de um reservatório de água com 5   m de altura perfurando um orifício bem arredondado com 3   c m   de diâmetro com perda desprezível na superfície inferior e

anexando uma curva horizontal de 90 ° com comprimento desprezível. Tomando o fator de correção da energia cinética como 1,05 , determine a vazão da água através da curva se :

  1. A curva for suave e flangeada
  2. a curva for chanfrada e sem aletas.

Passo 1

Vamos lá! Queremos a vazão da água em duas condições diferentes que o exercício pediu pra a gente!

Primeiro de tudo vamos definir os pontos, em cima da superfície da água vai ser nosso ponto 1 e na saída da água, bem na pontinha do tubo vai ser o nosso ponto 2 .

Para achar a vazão vamos usar a equação de energia para esses dois pontos:

Estamos considerando um escoamento permanente, desenvolvido e incompressível!

P 1 ρ g + α 1 V 1     2 2 g + z 1 + h b o m b a = P 2 ρ g + α 2 V 2     2 2 g + z 2 + h t u r b i n a + h L

Agora vamos assumir algumas coisas!

  • Como o reservatório é aberto e a água escoa para a pressão atmosférica, podemos dizer que P 1 = P 2 = P a t m ;
  • Vamos determinar z 2 = 0 , dessa forma z 1 = 5 m ;
  • Como o reservatório tem grandes dimensões, V 1 ≅ 0 ;
  • Não temos nenhuma bomba e nenhuma turbina, logo h b o m b a / t u r b i n a   = 0 .

Passo 2

Aplicando na equação de energia:

z 1 = α 2 V 2     2 2 g + h L

A perca de carga, h L pode ser escrita como:

h L = K L × V 2   2 2 g

Substituindo:

z 1 = α 2 V 2     2 2 g + K L × V 2     2 2 g

Agora vamos dar uma arrumadinha e isolar a velocidade:

V 2 = 2 g z 1 α 2 + K L  

Agora que podemos achar a velocidade a gente precisa saber como usar essa informação para chegar na vazão, que é o que queremos:

V ˙ = A 2 V 2

Substituindo:

V ˙ = π D 2 4 × 2 g z 1 α 2 + K L  

O K L vai ser diferente para cada situação que o exercício pediu, esse valor é tabelado.

Passo 3

Vamos então substituir o que descobrimos até aqui nos casos que o exercício propôs!

  1. A curva for suave e flangeada

    2. Nesse caso K L = 0,3   , substituindo nessa equação aqui:

    V ˙ = π D 2 4 × 2 g z 1 α 2 + K L  

    V ˙ = π ( 0,03 ) 2 4 × 2 ( 9,81 ) ( 5 ) 1,05 + 0,3 = 0,00603   m 3 / s    

    Ou:

    V ˙ = 6,03   L / s

    Agora vamos substituir para o segundo caso:

  2. a curva for chanfrada e sem aletas.

Agora K L = 1,1

V ˙ = π ( 0,03 ) 2 4 × 2 ( 9,81 ) ( 5 ) 1,05 + 1,1 = 0.00478   m 3 / s    

Ou:

V ˙ = 4,78   L / s

Prontinhoo!

Resposta

  1. V ˙ = 6,03   L / s .
  2. V ˙ = 4,78   L / s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema série-paralelo da figura a seguir, todos os tubos são de ferro fundido asfaltado de 8 cm de diâmetro. Se a queda total de pressão p 1 - p 2 = 750k P a , determine a vazão resultante Q e
Modifique o problema P6.113 da seguinte maneira: Considere a bomba ligada e deixando 45 kW para a vazão no tubo 2. O fluido é gasolina a 20°C. Determine (a) a vazão em cada tubo e (b) a queda de press
O sistema de tubos de aço galvanizado em paralelo da figura abaixo fornece água a 20°C com uma vazão total de 0, 036 m³/s. Se a bomba está totalmente aberta, mas desligada, com um coeficiente de perda
Na figura abaixa, encontram-se 38 m de tubo de 50 mm, 23 m de tubo de 150 mm e 46 m de tubo de 75 mm, todos de ferro fundido. Há também três cotovelos de 90° e uma válvula globo aberta, todos flangead
O sistema de três reservatórios da figura abaixo fornece água a 20°C. Os dados do sistema são: D 1 = 200m mD 2 = 150m m D 3 = 225m m L 1 = 549m mL 2 = 366m mL 3 = 488m m Todos os tubos são de aço galv