Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 107

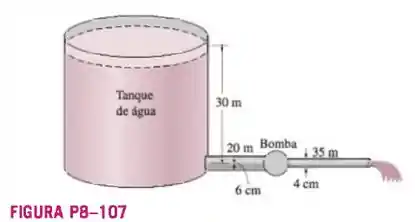
Água a 15 ° C deve ser descarregada de um reservatório a uma taxa de 18   L / s usando dois tubos de ferro fundido horizontais em série e uma bomba entre eles. O primeiro tubo tem 20   m   de comprimento e diâmetro de 6   c m , enquanto o segundo tubo tem 35   m de comprimento e 4   c m de diâmetro. O nível da água no reservatório é de 30   m acima do eixo central do tubo. A entrada do tubo tem aresta viva, e as perdas associadas à conexão da bomba são desprezíveis. Desprezando o efeito do fator de correção da energia cinética, determine a carga de bombeamento necessária e a potência de bombeamento mínima para manter a vazão indicada.

Passo 1

Para começar, vamos direto olhar a equação de energia! Assim a gente pode escolher os nossos pontos de acordo com as informações do enunciado!

Estamos considerando um escoamento permanente, desenvolvido e incompressível!

P 1 ρ g + α 1 V 1     2 2 g + z 1 + h b o m b a = P 2 ρ g + α 2 V 2     2 2 g + z 2 + h t u r b i n a + h L

O enunciado não da pra a gente nenhuma pressão, logo temos que escolher pontos onde a pressão é conhecida, eles são na superfície do tanque e na saída da água no tubo de ferro, nesses dois lugares a pressão é atmosférica!

Então, o ponto 1 é na superfície livre da água do tanque e o ponto 2 é na saída do tubo de ferro!!

Dessa forma, P 1 = P 2 .

Podemos dizer que V 1 = 0 , considerando as grandes dimensões do tanque.

Se definimos que a base do tanque tem altura 0 , podemos dizer que z 2 = 0 e z 1 = 30 m

O enunciado fala para a gente desprezar efeito do fator de correção da energia cinética, então α 1 = α 2 = 1 .

Não temos turbina, então h t u r b i n a = 0 .

Ficamos com a equação de energia da seguinte forma:

z 1 + h b o m b a = V 2     2 2 g + h L

A perda de carga h L é dada pelo somatório das perdas de carga maiores e menores:

h L = h m a i o r + h m e n o r

h L = ∑ ( f L D + ∑ K L   ) V 2 2 g

Passo 2

Temos dois tubos de ferro na saída, um antes da bomba e um depois da boba, eles tem diâmetros diferentes, portanto temos de calcular a perda de carga em cada um deles:

Vamos primeiro fazer os calculos para o tubo 1:

Vamos descobrir a velocidade para depois encontrarmos o Reynolds:

V t 1 = V ˙ A c 1 = V ˙ π D 1 2 4

Do enunciado:

V ˙ = 18 L s × 1 m 3 10 3 L = 18 × 10 - 3 m 3 / s

Também temos:

D 1 = 6   c m = 6 × 10 - 2   m

Substituindo:

V t 1 = 18 × 10 - 3 π 6 × 10 - 2 2 4 = 6,366   m / s

Calculando o número de Reynolds:

R e 1 = ρ V t 1 D 1 μ

O enunciado diz que a água esta a 15 ℃ , consultando tabelas achamos que ρ = 999,1   k g / m 3 e μ = 1,138 × 10 - 3 k g / m   s .

Calculando Reynolds:

R e 1 = 999,1 × 6,366 × 6 × 10 - 2 1,138 × 10 - 3 = 335300

Se Reynolds é maior que 4000 então o escoamento é turbulento!

A rugosidade, ε , pode ser achada em uma tabela, para um tubo de ferro ε = 0 , 00026 .

Calculando a rugosidade relativa:

ε L = 0 , 00026 20 = 0.00433

Consultando o diagrama de Moody achamos f 1 ≅ 0,03 .

Com isso podemos calcular a perda de carga total para o primeiro tubo h L 1 :

h L 1 = ( f L D + ∑ K L   ) V 2 2 g

Sabendo que K L = 0,5 para a entrada do tubo tem aresta viva, o enunciado diz para ignorarmos as perdas nas conexões da bomba!

Substituindo:

h L 1 = 0,03 20 0,06 + 0,5 6,366 2 2 × 9,81 = 21,69   m

Passo 3

Agora vamos fazer a mesma coisa, só que pro segundo cano!

A vazão volumétrica é igual a do primeiro cano, isso porque o escoamento é incompressível. Mas como o diâmetro muda, D 2 = 4   c m = 4 × 10 - 2 , a velocidade também muda!

V t 2 = 18 × 10 - 3 π 4 × 10 - 2 2 4 = 14,32   m / s

R e 2 = 999,1 × 14,32 × 4 × 10 - 2 1,138 × 10 - 3 = 502900

Calculando a rugosidade relativa para D 2 = 0,04   m   , lembrando que o tubo também é de ferro então ε = 0 , 00026 .

ε L = 0,00026 0,04 = 0,0065

Agora vamos pegar esses dados para procurar o fator de atrito f 2 no diagrama de Moody!

Achamos f 2 ≅ 0,032 .

Nesse caso não temos perdas menores, sabendo que o comprimento do tubo L 2 = 35   m podemos calcular h L 2 :

h L 2 = 0,032 35 0,04 14,32 2 2 × 9,81 = 292,6   m

Passo 4

Podemos calcular a perda de carga total:

h L = 21,69 + 292,6 = 314,29   m  

Mas o que queremos é h b o m b a e W ˙ b o m b a , então vamos voltar na equação de energia:

z 1 + h b o m b a = V 2     2 2 g + h L

Sabendo que z 1 = 30   m , V 2 = V t 2 = 14,32   m / s , podemos calcular:

h b o m b a   = 14,32 2 2 × 9,81 + 314,29 - 30 = 294,74   m

Para calcular a potência mínima da bomba, fazemos:

W ˙ b o m b a = V ˙ Δ P

O Δ P é dado por:

Δ P = ρ g h b o m b a

Calculando:

W ˙ b o m b a = 999,1 × 9,81 × 294,74 × 18 × 10 - 3 = 51998 W

Ou:

W ˙ b o m b a = 5 2   k W

Resposta

h b o m b a = 294,74   m

W ˙ b o m b a = 52   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três tubos de ferro fundido são colocados em paralelo com as seguintes dimensões:A vazão total é 200 m³/h de água a 20°C. Determine (a) a vazão em cada tubo e (b) a queda de pressão através do sistema
Para o problema 6.131, considere que, por questões de espaço, estejamos limitados a um comprimento total do difusor de 10 m. Qual seria o ângulo do difusor, o diâmetro e a pressão de saída para recupe
Uma seção de teste de um túnel de água tem 1 m de diâmetro e as propriedades do escoamento são V = 20m / s , p = 100k P a e T = 20 ° C . O bloqueio da camada limite no final da seção é 9%. Se um difus
Um soprador fornece ar a 3000 m³/h ao circuito de dutos da figura abaixo. Todos os dutos são de aço comercial e de seção transversal quadrada, com lados a 1 = a 3 = 20c m e a 2 = a 4 = 12c m . Admitin
Modifique o problema 6.118 como se segue. Admita que a queda de pressão p 1 - p 2 seja de 675, 7 kPa. Desprezando as perdas localizadas, determine a vazão em m³/h.