Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 66
Um suporte de mancal, com formas aerodinâmicas, encontra-se exposto ao escoamento de ar quente da exaustão de um motor. É necessário executar experimentos para determinar o coeficiente de transferência de calor por convecção médio entre o ar e o suporte, a fim de ser possível prever o resfriamento do suporte até uma temperatura superficial desejada . Decidiu-se efetuar experimentos de transferência de massa em um objeto com o mesmo formato do original e, com base nos dados coletados, obter os resultados desejados para a transferência de calor usando-se a analogia entre as transferências de calor e de massa.
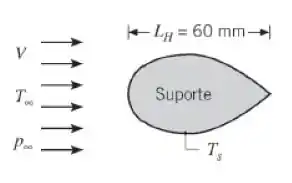
Os experimentos de transferência de massa foram conduzidos usando-se um modelo em meia escala do suporte, construído em naftaleno e exposto a uma corrente de ar a 27°C. As medidas de transferência de massa forneceram os seguintes resultados:
- Usando os resultados experimentais da transferência de massa, determine os coeficientes C e m para uma correlação com a forma
- Determine o coeficiente de transferência de calor por convecção médio para o suporte com o tamanho original, , quando ele estiver exposto a uma corrente livre de ar com , com .
- A área superficial do suporte pode ser representada por sendo o comprimento normal à página. Para as condições da parte (b), qual será a variação na taxa de transferência de calor para o suporte se o comprimento característico for dobrado?
Passo 1
E ai galerinha bonitaaa!!
Animados para mais uma??
Nós temos a seguinte situação:
E queremos achar m e C, porém nós não temos Sc, certo?
Então o que nós faremos aqui é a divisão entre dois pontos, já as condições de pressão e temperatura não mudaram o número de Sc e C serão constantes para ambos os pontos, usando 2 e 3
Usando artifícios matemáticos:
Usando os dados da tabela:
Belezaa!! Achamos o m e agora vamos partir para C, só que neste caso nós precisamos do número de Schmidt, ok?
Quando a temperatura e a pressão são 300 K e 1 atm, respectivamente, nós teremos::
Sendo assim:
Substituindo os dados para o ponto 2:
Substituindo:
E finalizamos a letra (a)!!
Passo 2
Para a letra (b) nós vamos levar em conta que, de forma análoga a nós temos .
Então:
Assim como:
Vamos lembrar que:
O que nós temos então é a seguinte fórmula:
Se o que nós queremos é o coeficiente:
O problema nos disse que:
Para a temperatura média entre nós podemos olhar na Tabela A.4 e obter:
Com tudo isso basta nós substituirmos:
E é só isso galerinhaa, letra (b) prontinhaa !!
Passo 3
A taxa de transferência de calor que nós queremos aqui na letra (c) é dada por:
Já sabemos que:
Ou seja:
Mas nós vimos que o coeficiente também está em função do comprimento, não foi?
Considerando apenas nossa variável:
Então o calor será proporcional, em relação apenas ao comprimento:
Quando nós dobramos:
Concluindo que, quando nós aumentamos o comprimento em duas vezes o calor é multiplicado por uma taxa de 1,74 !
E chegamos ao fim de mais umaa !!