Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 72
Na primavera, muitas vezes superfícies de concreto, como calçadas e estradas, ficam muito molhadas no período da manhã, mesmo na ausência de chuva durante a noite. Condições típicas para o período noturno são mostradas na figura.
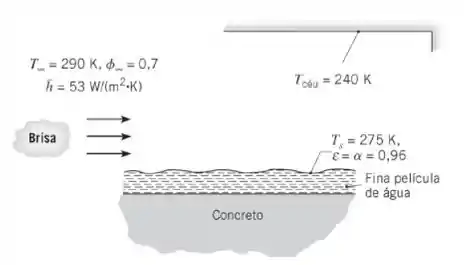
- Determine os fluxos térmicos associados à convecção, , à evaporação, , e à troca radiante com o céu, .
- Os seus cálculos sugerem a razão do concreto estar molhado ao invés de seco? Explique sucintamente.
- O calor flui da película de líquido para o concreto? Ou do concreto para a camada de líquido? Determine o fluxo térmico condutivo entrando ou saindo do concreto.
Passo 1
Vamooo que vaaaamo, galerinhaaa !!
Na letra (a) nós precisamos achar certo?
Vamos ver como calcular cada uma delas:
Se:
Então:
Sabemos que:
Olhando a Tabela A.6 para a água na superfície:
E no ambiente:
Levando em conta a umidade:
Nós ainda precisamos do coeficiente de transferência de massa médio, mas nós só temos o coeficiente de transferência de calor, então precisamos relacioná-los:
Onde é a densidade, o calor específico a pressão constante, o número de Lewis.
O número de Lewis também pode ser escrito como:
Onde é a difusividade térmica e a difusividade mássica!!
Para a maioria das aplicações
Sabendo que:
Na Tabela A.4 para nossa temperatura média de:
Nós não temos os valores exatos, mas podemos interpolar:
E na Tabela A.8 para o vapor de água e o ar podemos usar a relação dada:
Substituindo:
Bora calcular o calor?
Passo 2
Já o calor por convecção é calculado como:
E a transferência de calor por radiação será dada como:
Lembrando que:
Chegamos ao fim da letra (a) e agora vamos seguir pra (b) !!
Passo 3
Na letra (b) nós precisamos explicar porque o concreto estará molhado ao invés de seco!
E aí?!
Nós vimos que o calor de evaporação é negativo, certo? O que indica que ao invés de evaporação nós teremos condensação da água na superfície do concreto !1
E, por isso, ele estará molhado ao amanhecer !
Passo 4
Para finalizar com chave de ouro nós vamos para a letra (c) !!
Aqui nós queremos qual o fluxo térmico condutivo entrando ou saindo do concreto e vamos descobrir isso fazendo o balanço energético para o filme.
Sabendo que o filme estará recebendo calor por convecção e perdendo calor por condução, por radiação e por meio da evaporação:
Substituindo:
O que nos diz que o calor esta sendo adicionado ao concreto !!
E chegamos ao fim de mais umaa !!