Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 6.Problemas - Ex. 55
Um suporte de mancal, com formas aerodinâmicas, encontra-se exposto ao escoamento de ar quente da exaustão de um motor. É necessário executar experimentos para determinar o coeficiente de transferência de calor por convecção médio entre o ar e o suporte, a fim de ser possível prever o resfriamento do suporte até uma temperatura superficial desejada . Decidiu-se efetuar experimentos de transferência de massa em um objeto com o mesmo formato do original e, com base nos dados coletados, obter os resultados desejados para a transferência de calor usando-se a analogia entre as transferências de calor e de massa.
Os experimentos de transferência de massa foram conduzidos usando-se um modelo em meia escala do suporte, construído em naftaleno e exposto a uma corrente de ar a . As medidas de transferência de massa forneceram os seguintes resultados:
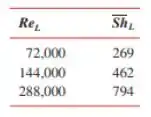
(a) Usando os resultados experimentais da transferência de massa, determine os coeficientes e para uma correlação com a forma .
(b) Determine o coeficiente de transferência de calor por convecção médio para o suporte com o tamanho original, , quando ele estiver exposto a uma corrente livre de ar com , e , com .
(c) A área superficial do suporte pode ser representada por , sendo l o comprimento normal à página. Para as condições da parte (b), qual será a variação na taxa de transferência de calor para o suporte se o comprimento característico for dobrado?
Passo 1
Bora resolver mais uma questão juntos!
Começamos o nosso problema explicitando a nossa equação:
Letra a)
Queremos obter , mas não possuímos .
Então, devemos fazer uma divisão entre dois pontos, como as condições de temperatura e pressão não mudam, teremos o mesmo e , assim, utilizando os pontos 2 e 3:
Aplicando em ambos os lados:
Substituindo com os dados da tabela fornecida pelo enunciado:
Agora, devemos calcular o coeficiente , mas para isso devemos obter primeiro.
Pelas Tabelas A.4 e A.8 à e , temos:
Assim:
Agora sim, calculando , utilizando o ponto 2:
Passo 2
Letra b)
Aqui, devemos levar em conta que ) e .
Então:
E
Temos também que:
E
Substituindo essas relações:
Como queremos :
Dados:
Pela Tabela A.4 para a temperatura aproximada de , temos:
Substituindo os dados na nossa equação:
Passo 3
Letra c)
A taxa de transferência de calor que nós queremos aqui é dada por:
Sabemos que:
Ou seja:
Mas vimos no Passo 2 que o coeficiente de transferência de calor também pode estar em função do comprimento:
Assim:
Então:
Quando dobramos:
Ufa, terminamos a nossa questão!
Até a próxima!