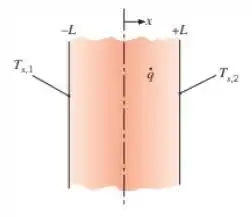
Considere uma parede plana unidimensional de 2 L de espessura que experimenta geração de calor volumétrico uniforme. As temperaturas da superfície da parede são mantidas em T s , 1 e T s , 2 como mostrado no esboço. Verificar por substituição direta, que uma expressão da formaSatisfaz a forma de estado estacionário da equação de difusão de calor. Determine uma expressão para a distribuição do fluxo de calor, q ' ' ( x ) .

S a t i s f a z ! q ' ' x = q ˙ x - k T s , 2 - T s , 12 L

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 19

Considere uma parede plana unidimensional de de espessura que experimenta geração de calor volumétrico uniforme. As temperaturas da superfície da parede são mantidas em e como mostrado no esboço. Verificar por substituição direta, que uma expressão da forma

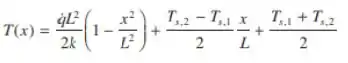
Satisfaz a forma de estado estacionário da equação de difusão de calor. Determine uma expressão para a distribuição do fluxo de calor, .

Passo 1

E aí, pronto para resolvermos essa questão?

Vamos lá!

Começamos o nosso problema verificando por substituição direta, que a expressão dada satisfaz a forma de estado estacionário da equação de difusão de calor:

Substituindo a equação dada:

Integrando:

Integrando novamente:

Passo 2

Determinando uma expressão para a distribuição do fluxo de calor, :

Substituindo a equação dada:

Integrando:

E assim finalizamos a nossa questão, te espero na próxima!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Condução unidimensional, em regime estacionário, com geração de energia interna uniforme ocorre em uma parede plana com espessura de 50m m e condutividade térmica constante igual a 5W / ( m·K ) . Ness

A distribuição de temperaturas, em regime estacionário, em um material semitransparente, com condutividade térmica k e espessura L , exposto à irradiação laser é descrita por T x = - A k a 2 e - a x +

Em um elemento combustível cilíndrico para reator nuclear, com 50m m de diâmetro, há geração interna de calor a uma taxa uniforme deq ̇ =5×10 7W / m 3 . Em condições de regime estacionário, a distribu

Em uma parede plana com espessura 2 L=40m m e condutividade térmica k=5W / ( m·K ) há geração de calor volumétrica uniforme a uma taxa q ˙ , enquanto transferência de calor por convecção ocorre em sua

Uma placa plana fina de comprimento L, espessura t e largura W ≫L está termicamente ligada a dois grandes sumidouros de calor, que são mantidos a uma temperatura T e . A superfície inferior da placa e