Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fundamentos de Transferência de Massa - Marco Aurélio Cremasco- Ed: 2º - Capítulo 8.Conceitos - Ex. 18
Demonstre, para teoria da camada limite, que , em
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro de fundamentos e transferência e massa do cremasco ele pede para demonstrar para teoria da camada limite, que , em
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Para demonstrar que,
, com
Temos sua representação laminar formulada por,
Seguindo a análise do gráfico,
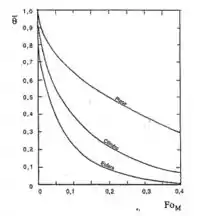
Ficando,
Com isso a teoria da camada limite fica determinado por,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
Exercícios de Livros Relacionados
A fotossíntese, como ocorre nas folhas de uma planta verde, envolve o transporte de dióxido de carbono ( C O 2 ) da atmosfera para os cloroplastos das folhas. A taxa de fotossíntese pode ser quantific
Sabe-se que em noites limpas a temperatura do ar não precisa ser inferior a 0 ° C para que uma fina camada de água sobre o solo se congele. Considere uma dessas camadas de água sobre o solo em uma noi
Um suporte de mancal, com formas aerodinâmicas, encontra-se exposto ao escoamento de ar quente da exaustão de um motor. É necessário executar experimentos para determinar o coeficiente de transferênci
Uma camada de água, com 1m m de espessura, sobre uma placa eletricamente aquecida é mantida a uma temperatura de T a = 340K , enquanto ar seco a T ∞ = 300K escoa sobre a sua superfície (caso A). O con
A seção de secagem de uma fábrica de papel consiste em 30 rolos cilíndricos de 1,5m de diâmetro e 3m de comprimento. Um arco de 225° de cada rolo está em contato com a folha de papel úmido, enquanto a