Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 75
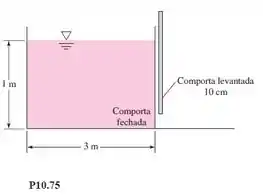
Um tanque de água com 1 m de profundidade, 3 m de comprimento e 4 m de largura no sentido perpendicular ao papel tem uma comporta de fundo fechada no lado direito, como mostra a Figura P10.75. Em a comporta é aberta com uma abertura de 10 cm. Considerando a teoria quase-permanente da comporta de fundo, calcule o tempo necessário para que o nível da água caia a 50 cm. Suponha descarga livre.
Passo 1
E simbora!
Partindo da equação 10.41, teremos:
Tendo,
Como cai de 1,0 para 0,5 m, teremos que vai cair devagar de para 0,576. Porém, vamo assumir aproximadamente constante com um valor de 0,584, assim, ao aplicar separação de variáveis:
Em que,
Resolvendo K, temos:
Tendo e , encontraremos que:
Resposta
Exercícios de Livros Relacionados
Água, escoando horizontalmente em um canal largo de profundidade de 30c m , passa por um ressalto hidráulico cuja dissipação de energia é de 71 % . Calcule (a) a profundidade a jusante e (b) a vazão v
Água escoa em um canal largo a q = 2,32 m 3 s ⋅ m ,y 1 = 0,3m , e então passa por um ressalto hidráulico. Calcule y 2 ,V 2 ,F r 2 ,h p , o percentual de dissipação e a potência dissipada por unidade d
Repita o Problema P 10.75 se a comporta estiver afogada em y 2 = 40c m .
A Equação ( 10.41 ) vale para o coeficiente de descarga livre (quase sem atrito). Se a saída estiver afogada, como na Figura P 10.10 c , haverá dissipação e o C d cairá bruscamente. A Figura P 10.77 m
Água com 30c m de profundidade está em escoamento uniforme em um canal de concreto sem acabamento, em declive de 1 ° , quando ocorre um ressalto hidráulico, como na Figura P 10.89 . Se o canal for mui