Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 41
Determine o valor mais eficiente de para o canal em forma de V da Figura P10.41.
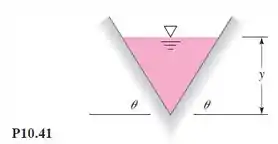
Passo 1
E simbora! Vamo fazer isso ficar simples!
Temos as relações para essa figura sendo,
Vamos eliminar y, assim:
Derivando e igualando a zero para encontrar o máximo valor de eficiência, teremos:
De boas né?! O macete era só pegar a área e o perímetro e fazer a relação colocando o perímetro em evidencia!
Resposta
Exercícios de Livros Relacionados
13-80 A profundidade do escoamento e a velocidade da água medidas após um salto hidráulico são 2 m e 3 m/s, respectivamente. Determine a profundidade e velocidade de escoamento antes do salto, e a fra
13-85C Considere o escoamento de um líquido sobre uma saliência durante o escoamento subcrítico em um canal aberto. A energia específica e a profundidade do escoamento diminuem sobre a saliência à med
13-86C O que é um reservatório de soleira espessa? Qual é a base de classificação dos reservatórios de soleira espessa?
13-87 A água é liberada de um reservatório com 14 m de profundidade em um canal aberto com 6 m de largura através de uma comporta basculante com uma abertura de 1 m de altura no fundo do canal. Se a p
13-88 A água que escoa em um canal largo encontra uma saliência de 22 cm de altura no fundo do canal. Se a profundidade de escoamento for de 1,2 m e a velocidade de 2,5 m/s antes da saliência, determi