Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 77
A Equação vale para o coeficiente de descarga livre (quase sem atrito). Se a saída estiver afogada, como na Figura , haverá dissipação e o cairá bruscamente. A Figura mostra os dados da sobre comportas de fundo verticais afogadas. Use este diagrama para repetir o Problema e traçar a vazão calculada em função de no intervalo .
Passo 1
E aí, tudo bem? Bora matar essa questão!
Primeiro precisamos pegar todos os coeficientes para uma única linha vertical, assim:
Logo não terá efeito de afogamento, até que:
Agora temos que:
Bem como querendo a variação entre
Passo 2
b)
Vamos montar um gráfico para o nosso problema, lembrando que:
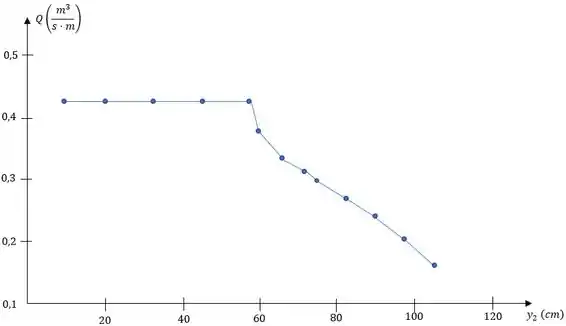
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Gráfico vide passo a passo
Exercícios de Livros Relacionados
O canal retangular da Figura P10.120 contém um vertedouro com entalhe em V. O objetivo é medir vazões entre 2,0 m3/s e 6,0 m3/s com uma ponta linimétrica do tipo gancho a montante, medindo profundidad
Usando uma análise do tipo Bernoulli semelhante à da Figura 10.16a, mostre que a vazão teórica do vertedouro em formato de V na Figura P10.118 é dada por Q = 0,7542 g 1 / 2 tan α H 5 / 2
Um dispositivo popular para medir vazão na agricultura é a calha Parshall [33], Figura P10.117, que recebeu esse nome em homenagem ao seu inventor, Ralph L. Parshall, que a desenvolveu em 1922 para o
PP10.1 – Um canal reto em terra com vegetação rasteira tem um formato trapezoidal da Fig. 10.7, com b = 4 m e θ = 35°. O canal tem uma declividade de fundo constante de 0,001. A vazão varia sazonalmen
PP10.2 – A barragem Caroselli no Rio Pawcatuck tem 3 m de altura, 27,4 m de largura e a borda aguda. A companhia Coakey usa essa altura para gerar potência hidrelétrica e quer mais potência. Eles soli