Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 139

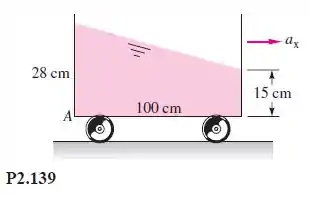
O tanque de líquido da Figura P2.139 acelera para a direita com o fluido em movimento de corpo rígido. (a) Calcule a x em m / s 2 . (b) Por que a solução da parte (a) não depende da massa específica do fluido? (c) Determine a pressão manométrica no ponto A se o fluido for glicerina a 20 ℃ .

Passo 1

Tudo Certo pessoal?? Bora resolver mais essa questão comigo??

(a) Para encontramos a aceleração, podemos usar a inclinação do líquido, assim, temos que:

tan ⁡ θ = a x g

Como a tangente de um angulo pode ser dado pelo cateto oposto divido pelo cateto adjacente, podemos dizer que:

tan ⁡ θ = 28   c m - 15   c m 100   c m   = 0,13

Substituindo, temos:

a x = g tan ⁡ θ

a x = 9,81   m / s 2 0,13

a x = 1,28     m / s 2

Passo 2

(b) Claramente, a solução para (a) é puramente geométrica e não envolve densidade de fluido.

Passo 3

(c) Da Tabela A-3 para glicerina, temos que a densidade é:

ρ   =   1260   k g / m 3

Existem muitas maneiras de calcular p A . Por exemplo, podemos ir direto para o lado esquerdo, usando apenas a gravidade:

p A = ρ g Δ z

p A = ( 1260   k g / m 3 ) ( 9,81   m / s 2 ) ( 0,28   m )  

p A = 346 1   P a

Ou podemos começar do lado direito, descer 15   c m com g e através de 100   c m com a x :

p A = ρ g Δ z + ρ a x Δ x

p A = ( 1260   k g / m 3 ) ( 9,81   m / s 2 ) ( 0 , 15   m )   + ( 1260   k g / m 3 ) ( 1,28     m / s 2 ) ( 1   m )

p A = 3467   P a

Resposta

(a)

a x = 1,28     m / s 2

(c)

p A = 346 1   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A fish tank 14 in deep by 16 by 27 in is to be carried in acar that may experience accelerations as high as 6 m/s2.What is the maximum water depth that will avoid spillingin rigid-body motion? What is
Suppose that the U-tube of Fig. P2.151 is rotated about axisDC. If the fl uid is water at 1228F and atmospheric pressure is 2116 lbf/ft2 absolute, at what rotation rate will the fluid withinthe tube b
The tank of water in Fig. P2.143 is full and open to the atmosphere at point A. For what acceleration ax in ft/s2 will thepressure at point B be (a) atmospheric and (b) zero absolute?
The 6-ft-radius waterwheel in Fig. P2.149 is being used tolift water with its 1-ft-diameter half-cylinder blades. If thewheel rotates at 10 r/min and rigid-body motion is assumed,what is the water sur
Figure P2.160 shows a gage for very low pressures, invented in 1874 by Herbert McLeod. (a) Can you deduce,from the fi gure, how it works? (b) If not, read about it andexplain it to the class.