Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 149
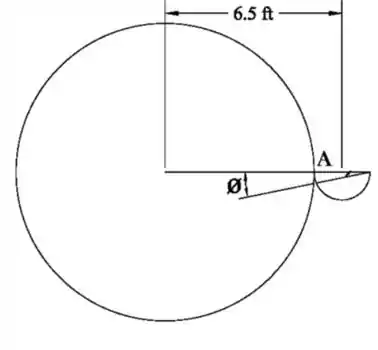
The 6-ft-radius waterwheel in Fig. P2.149 is being used to
lift water with its 1-ft-diameter half-cylinder blades. If the
wheel rotates at 10 r/min and rigid-body motion is assumed,
what is the water surface angle θ at position A?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Os dados são os seguintes:
Raio da roda:
Velocidade de rotação:
Passo 2
As lâminas estão funcionando como baldes para levantar água. E também meio-cilindros com diâmetro. Todo o sistema está em movimento de corpo rígido. Como o movimento do corpo rígido é assumido no local de se a superfície da água faz uma inclinação, obtemos:
Aqui denota a velocidade angular da caçamba semicilíndrica no raio
Passo 3
Substituindo os valores que obtemos,
Então a água no balde faz um ângulo .