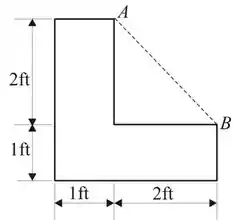
The tank of water in Fig. P2.143 is full and open to the atmosphere at point A. For what acceleration ax in ft/s2 will the

pressure at point B be (a) atmospheric and (b) zero absolute?

Assumimos que a água dentro do tanque está em movimento rígido do corpo e não há derramamento de água.

Tanque está aberto à atmosfera no ponto .

(a) Quando a pressão no ponto é atmosférica Ambos os pontos e estão à pressão atmosférica

Vamos unir pontos e por uma linha imaginária e isso se assemelha a uma linha de pressão constante

Quando o contêiner está se movendo de forma constante, então

Como não há aceleração ao longo da direção, assumimos . Substituindo os valores conhecidos na equação acima:

Portanto, o tanque é acelerado quando a pressão no ponto é atmosférica

(b) Quando a pressão no ponto é zero absoluta.

A pressão no ponto é zero absoluta, entendemos que a pressão do medidor no ponto é Agora o ponto é em direção à direção da aceleração do ponto , obtemos

Das propriedades dos lençóis freáticos, a densidade da água é

Então

Assim, o tanque deve acelerar em direção à direita quando a pressão no ponto é zero