Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 10

Se a tensão superficial γ for incluída na analise do problema P10.9, a velocidade de onda resultante é

c 0 2 = g λ 2 π + 2 π γ ρ λ tanh ⁡ 2 π y λ

(a) Determine se essa expressão é afetada pelo número de Reynolds, número de Froude ou número de Weber. Deduza os valores-limite dessa expressão para (b) y ≪ λ e (c) y ≫ λ . (d) Finalmente, determine o comprimento de onda λ c r i t para um valor mínimo de c 0 , supondo que y ≫ λ .

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Essa questão vai exigir da gente lembrar muito forte da parte teórica das paradas!

(a) Não há efeitos na teoria para o número de Reynolds ou de Weber, porque a viscosidade e a tensão superficial não estão presente na fórmula. Há um efeito no número de Froude, e podemos reescrever como um número de Froude versus uma profundidade adimensional, se liga!

F r o n d a = c 0 g λ = 1 2 π + 2 π γ ρ g λ 2 tanh ⁡ 2 π y λ = f y λ ,   W e

Onde W e = ρ g λ 2 γ

Passo 2

(b) y ≪ λ :

tanh ⁡ ζ ≈ ζ

Se ζ ≪ 1 :

c o ,   o n d a s   l o n g a s 2 = g y + 4 π 2 γ y ρ λ 2

Passo 3

(c) y ≫ λ :

tanh ⁡ ζ ≈ 1

Se ζ ≫ 1 :

c o ,   o n d a s   c u r t a s 2 = g λ 2 π + 2 π γ ρ λ

Passo 4

(d) O comprimento de onda crítico pode ser obtido a partir da equação encontrada no passo (3) e derivando-o em função do comprimento de onda e igualando nossa equação a zero!!!

d c 0 2 d λ = g 2 π - 2 π γ ρ λ 2 = 0

λ c r í t i c o = 2 π γ ρ g

Onde c o = c o ,   m í n

Portanto, temos nossa equação de comprimento de onda crítico. Agora vamos ficar variando λ para saber qual deve ser esse valor. Eu vou montar um gráfico porque fica mais fácil de enxergar!!!

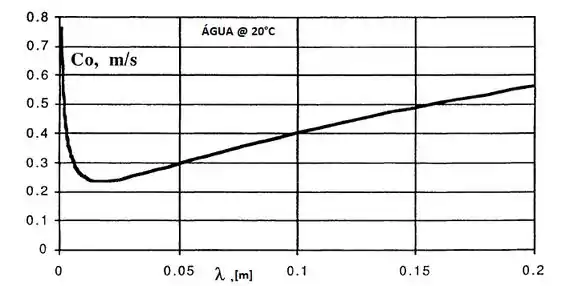
O valor crítico é em 0,018 cm

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento subsônico de Fanno do ar com número de entrada de Mach 0,70. Se o número de Mach aumentar para 0,90 na saída do duto como resultado do atrito, a (a) temperatura de estagnação T
Considere o escoamento subsônico de Fanno do ar com número de entrada de Mach 1,8. Se o número de Mach aumentar para 1,2 na saída do duto como resultado do atrito, a (a) temperatura de estagnação T 0
Qual é o efeito do atrito sobre a velocidade do escoamento no escoamento subsônico de Fanno? Responda a mesma pergunta para o escoamento supersônico de Fanno.
Considere o escoamento subsônico de Fanno acelerado até a velocidade sônica (Ma = 1) na saída do duto como resultado dos efeitos do atrito. Se o comprimento do duto aumentasse mais, o escoamento na sa
Considere o escoamento supersônico de Fanno desacelerado até a velocidade sônica (Ma = 1) na saída do duto como resultado dos efeitos do atrito. Se o comprimento do duto aumentasse mais, o escoamento