Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas Abrangentes - Ex. 3

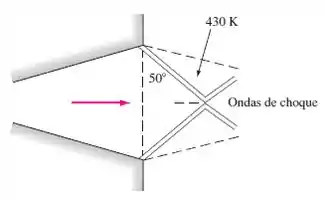
A figura abaixo mostra a saída de um bocal convergente-divergente, em que um padrão de choque oblíquo é formado. No plano de saída, que tem uma área de 15 cm², a pressão do ar é de 16 kPa e a temperatura é de 250 K. Exatamente fora do choque de saída, que faz um ângulo de 50° com o plano de saída, a temperatura é d 430 K. Calcule (a) a vazão em massa, (b) a área da garganta, (c) o ângulo de deflexão do escoamento de saída, e, no tanque de abastecimento de ar, (d) a pressão e (e) a temperatura.

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Bem, conhecemos qual é a razão das temperaturas no ponto 1 no ponto 2. Também sabemos qual é o ângulo da onda de choque, então temos:

T 2 T 1 = 430 250 = 1,72

β = 40 °

Vamos ter que iterar a equação 9.83 (que se você olhar no livro é um combo de equações)

Passo 2

De forma geral, teremos ao final que

M a s = 3,17

ρ 1 = 0,223   k g / m ³

A 1 A * = 4,99 = 15 A g a r g a n t a → A g a r g a n t a = 3   c m ²

V 1 = M a 1 a 1 = 1006 m s

m ˙ = ρ 1 A 1 V 1 = 0,336 k g s

θ c h o q u e = 22 ,   88 °

Passo 3

O número de Mach na saída é conhecido agora, então fica fácil de calcularmos as condições de estagnação!!

p o , t a n q u e = 16 1 + 0,2 3,17 2 3,5 = 760   k P a

T o , t a n q u e = 250 1 + 0,2 3,17 2 = 753   K

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com relação ao Problema P3.68, mostre que o empuxo de um motor-foguete descarregando no vácuo é dado por F = p o A s 1 + k M a s 2 1 + k - 1 * M a s 2 2 k k - 1 em que A s = área de saída M a s = núme
Ar em um tanque a 120 kPa e 300 K descarrega para a atmosfera por um bocal convergente com garganta de 5 cm² a uma taxa de 0,12 kg/s. Qual é a pressão atmosférica? Qual é a máxima vazão em massa possí
A orientação de um furo pode fazer diferença. Considere os furos A e B na Figura P9.78, que são idênticos mas invertidos. Para as propriedades do ar dadas em ambos os lados, calcule a vazão em massa a
Um grande tanque a 500 K e 165 kPa fornece ar a um bocal convergente. A contrapressão externa à saída do bocal é o padrão ao nível do mar. Qual é o diâmetro de saída adequado se a vazão em massa desej
Um grande reservatório a 600 K fornece ar a um bocal convergente-divergente com área de garganta de 2 cm². Uma onda de choque normal se forma em uma seção de área de 6 cm². Exatamente a jusante desse