Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 16

Trabalhe o Problema 3.15 supondo que as superfícies paralelas à direção x sejam adiabáticas.

Passo 1

Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.

A transferência de calor ocorre em apenas em uma direção, como mostra o esquema ilustrativo abaixo:

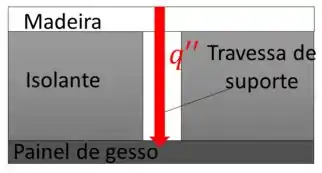
Esse problema difere do anterior em apenas uma coisa: temos aqui uma parede cujas superfícies paralelas a x são adiabáticas e, portanto, devemos dividir a parede da seguinte maneira:

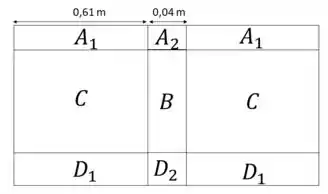
Devemos, então, encontrar a resistência térmica total da parede, depois de esboçar o circuito térmico associado ao volume de controle que vamos analisar.

Antes de ir para os próximos passos, devemos procurar as condutividades térmicas de todos os materiais utilizados na composição da parede: madeira (material da placa superior e da travessa de suporte), fibra de vidro (material do isolante) e gesso (material do painel inferior).

Indo na Tabela A.3 (página 629) encontramos as seguintes condutividades térmicas:

M a n d e i r a   d e   l e i   d u r a → k A = k B = 0,16 W m . K F i b r a   d e   v i d r o   ( 28   k g / m ³ ) → k C = 0,038 W m . K P l a c a   d e   g e s s o   →   k D = 0,17 W m . K

Por fim, antes de encerramos esse Passo 1, devemos nos atentar às dimensões dessa parede, da forma como eu mostrei na segunda imagem

Temos a divisão A 1 de espessura L A 1 = 8   m m =   0,008   m , uma largura W A 1 = 0,61   m e uma altura H A 1 = 2,5   m . Sendo assim, a área transversal dessa placa é A T , A 1 =   H A 1 ∙ W A 1 = 0,61   m ∙ 2,5   m = 1,525   m ² .

A divisão A 2 tem espessura L A 2 = 8   m m =   0,008   m , uma largura W A 2 = 0,04   m e uma altura H A 2 = 2,5   m . Sendo assim, a área transversal dessa placa é A T , A 2 =   H A 2 ∙ W A 2 = 0,04   m ∙ 2,5   m = 0,1   m ² .

Uma única travessa de madeira tem espessura L B = 130   m m =   0,13   m , uma largura W B = 40   m m = 0,04   m e uma altura H B = 2,5   m . Sendo assim, a área transversal de uma travessa é A T , B =   H B ∙ W B = 0,04   m ∙ 2,5   m = 0,1   m ² .

O isolante de fibra de vidro tem espessura L C = 130   m m =   0,13   m , uma largura W C =   0,61   m e uma altura H C = 2,5   m . Sendo assim, a área transversal do isolante é A T , C =   H C ∙ W C = 0,61   m ∙ 2,5   m = 1,525   m ² .

A divisão D 1 tem espessura L D 1       = 12   m m =   0,012   m , uma largura W D 1       = 0,61   m e uma altura H D 1       = 2,5   m . Sendo assim, a área transversal dessa placa é A T , D 1       =   H D 1       ∙ W D 1       = 0,61   m ∙ 2,5   m = 1,525   m ² .

A divisão D 2 tem espessura L D 2     = 12   m m =   0,012   m , uma largura W D 2       = 0,04   m e uma altura H D 2       = 2,5   m . Sendo assim, a área transversal dessa placa é A T , D 2       =   H D 2       ∙ W D 2       = 0,04   m ∙ 2,5   m = 0,1   m ² .

Passo 2

Olhando para o esquema apresentado na segunda imagem do Passo 1, e lembrarmos que uma resistência térmica pode ser escrita na forma R =   L / k A , sendo L a espessura da parede e k sua condutividade térmica e A a área, o circuito térmico para esse problema pode ser esquematizado como:

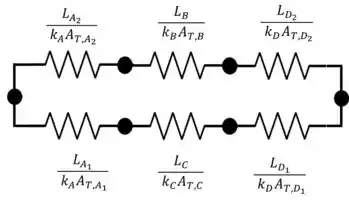
Pela imagem, devemos calcular duas resistências equivalentes em série:

R e q , 1 = R A 1 + R C + R D 1

R e q , 2 = R A 2 + R B + R D 2

Vamos calcular cada uma das resistências:

R A 1 = L A k A A T , A = 0,008   m 0,16 W m . K ( 1,525   m ² ) = 0,0328   K / W

R A 2 = L A k A A T , A = 0,008   m 0,16 W m . K ( 0,1   m ² ) = 0,5   K / W

R B = L B k B A T , B = 0,13   m 0,16 W m . K ( 0,1   m ² ) = 8,125   K / W

R C = L C k C A T , C = 0,13   m 0,038 W m . K ( 1,525   m ² ) = 2,243   K / W

R D 1 = L D 1 k D A T , D 1 = 0,012   m 0,17 W m . K ( 1,525   m ² ) = 0,0469   K / W

R D 2 = L D 2 k D A T , D 2 = 0,012   m 0,17 W m . K ( 0,1   m ² ) = 0,7059   K / W

Vamos calcular as duas resistências equivalentes em série:

R e q , 1 = 0,0328 K W + 2,243 K W + 0,0469 K W = 2,323   K W

R e q , 2 = 0,5 K W + 8,125 K W + 0,7059 K W = 9,331 K W

Agora, devemos calcular a resistência equivalente do circuito demonstrado como em paralelo:

1 R c i r c u i t o = 1 R e q , 1 + 1 R e q , 2 =   1 2,323   K W + 1 9,331 K W → R c i r c u i t o = 1,86 K W

Passo 3

Pra finalizar a questão, devemos agora lembrar que o enunciado afirma que a parede toda tem dez travessas. Ou seja, esse circuito para o qual acabamos de encontrar a resistência equivalente se repete dez vezes na parede.

Ou seja, para calcular a resistência total, devemos considerar dez desses circuitos em paralelo:

1 R t o t =   10 R c i r c u i t o → 1 R t o t = 10 1,86 K W → R t o t = 0,186   K W

Resposta

Como demonstrado no Passo 3, R t o t = 0,186   K W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As redes de resistência térmica também podem ser usadas aproximadamente para problemas multidimensionais. Para que tipo de problemas multidimensionais a abordagem de resistência térmica dará resultado
Ao desenhar uma rede de resistência térmica associada ao problema de transferência de calor, explique quando duas resistências estão em série e em paralelo.
Uma t��pica seção de parede de edifício é mostrada na Fig. P3–53. Esta seção se estende para dentro e para fora da parede e é repetida na direção vertical. Os membros de apoio de parede são feitos de
Reconsiderar Problema 3-54. Usando o EES (ou outro programa), trace a taxa de transferência de calor através da parede em função da espessura da espuma rígida na faixa de 1 a 10 cm. Discuta os resulta
Uma parede de 25 cm de espessura, 9 m de comprimento e 3 m de altura deve ser construída com tijolos k = 0,70 W m . K sólidos de 18c m × 18c m ou tijolos de dimensões idênticas com nove buracos de ar